题目内容
19.已知一个二元一次方程组的解是$\left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$,则这个方程组是( )| A. | $\left\{\begin{array}{l}2x=y\\ x+y=-3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=-3\\ x-2y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=-3\\ x-y=-2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=0\\ 3x-y=5\end{array}\right.$ |
分析 把x与y的值代入各方程组检验即可.
解答 解:A、把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第一个方程左边得:-2;右边为-2,左右两边相等;
把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第二个方程左边得:-1-2=-3;右边为-3,左右两边相等,
则此方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$;
B、把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第一个方程左边得:-1-2=-3;右边为-3,左右两边相等;
把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第二个方程左边得:-1+4=3;右边为1,左右两边不相等,
则此方程组的解不为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$;
C、把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第一个方程左边得:-1-2=-3;右边为-3,左右两边相等;
把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第二个方程左边得:-1+2=1;右边为-2,左右两边不相等,
则此方程组的解不为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$;
D、把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第一个方程左边得:-1-2=-3;右边为0,左右两边不相等;
把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入第二个方程左边得:-3+2=-1;右边为5,左右两边不相等,
则此方程组的解不为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$;
故选A
点评 此题考查了二元一次方程组的解,熟练掌握运算法则是解本题的关键.

 表示运算x+z-(y+w),则
表示运算x+z-(y+w),则 的结果是( )
的结果是( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
 如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F.
如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F. 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.
如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.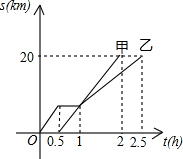 甲、乙从A出发,骑车沿同一条路行驶至B,他们离出发地的距离s(km)和时间t(h)间的函数图象如图所示,
甲、乙从A出发,骑车沿同一条路行驶至B,他们离出发地的距离s(km)和时间t(h)间的函数图象如图所示,