题目内容

8．解不等式组$\left\{\begin{array}{l}{7x-9≤4x-3}\\{6x+7＜11x+12}\end{array}\right.$，并将其解集在数轴上表示．

分析 先分别解两个不等式得到x≤2和x＞-1，再利用大小小大中间找确定不等式组的解集，然后利用数轴表示解集．

解答 解：$\left\{\begin{array}{l}{7x-9≤4x-3①}\\{6x+7＜11x+12②}\end{array}\right.$，
解①得x≤2，
解②得x＞-1，
所以不等式组的解集为-1＜x≤2，
用数轴表示为：

点评 本题考查了解元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．也考查了在数轴上表示不等式的解集．

练习册系列答案
相关题目
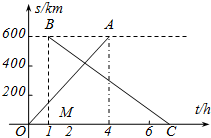18．甲、乙两城市之间开通了动车组高速列车．已知每隔2h有一列速度相同的动车组列车从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：
（1）从图象看，普通快车发车时间比第一列动车组列车发车时间晚1h（填“早”或“晚”），点B的纵坐标600的实际意义是甲、乙两城市之间的距离为600千米；
（2）请直接在图中画出第二列动车组列车离开甲城的路程s（km）与时间t（h）的函数图象；
（3）若普通快车的速度为100km/h，
①求BC的表达式，并写出自变量的取值范围；
②第二列动车组列车出发多长时间后与普通快车相遇？
③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔．
19．已知：关于的方程x2-（k+1）x+$\frac{1}{4}$k2+1=0的两根是一个矩形两邻边的长．
（1）求k实数的取值范围；
（2）当矩形的对角线长为$\sqrt{5}$时，求实数k的值．
16．三元一次方程组$\left\{\begin{array}{l}{3x-y+z=4}\\{2x+3y-z=12}\\{x+y+z=6}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$．
3．已知（2x-3y+1）2与|4x-3y-1|互为相反数，则x，y的值为（　　）
A．x=-1，y=1B．x=1，y=-1C．x=-1，y=-1D．x=1，y=1
13．计算：
（1）$\sqrt{32}$-4$\sqrt{\frac{1}{2}}$+$\frac{\sqrt{6}×\sqrt{3}}{\sqrt{2}}$
（2）$\sqrt{81}$-$\root{3}{-27}$+（3.14-π）0-|-$\sqrt{16}$|．
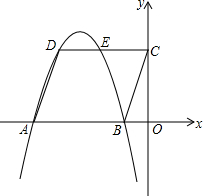20．已知：平行四边形ABCD在直角坐标系中的位置如图，O是坐标原点，OB：OC：OA=1：3：5，S□ABCD=12，抛物线经过D、A、B三点．
①求A、C两点的坐标；
②求抛物线解析式；
③E是抛物线与DC交点，以DE为边的平行四边形，它的面积与ABCD面积相等，且另两顶点为P、N中有一个顶点P在抛物线上．求P点和N点的坐标．
17．计算
（1）$-{2^3}×（{-8}）-{（{-\frac{1}{2}}）^3}×（{-16}）+\frac{4}{9}×{（{-3}）^2}$
（2）[（-3）2-（-5）2]÷（-8）+（-3）×（-1）
18．（x+3）（x-2）=x2+x-6；  （-6x2y4）3xy2=-18x3y6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网