题目内容
2.在平面直角坐标系中.(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4),若AB∥x轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段AB的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
分析 (1)根据y轴上点的横坐标为0解答可得;
(2)根据平行于x轴的直线纵坐标相等且第一象限内点的横纵坐标均为正数解答可得;
(3)由(2)中结论结合AB=6得出点A、B坐标,利用两点间的距离公式求出PA2、PB2,根据勾股定理逆定理求解可得.
解答 解:(1)根据题意知,2a-6=0,
解得:a=3,
∴点P的坐标为(0,7);
(2)∵AB∥x轴,
∴m-1=4,解得m=5,
∵点B在第一象限,
∴n+1>0,解得n>-1;
(3)由(2)知点A(-3,4),
∵AB=6,且点B在第一象限,
∴点B(3,4),
由点P(0,7)可得PA2=(-3-0)2+(4-7)2=18、PB2=(3-0)2+(4-7)2=18,
∵AB2=36,
∴PA2+PB2=AB2,且PA=PB,
因此,△PAB是等腰直角三角形.
点评 本题主要考查坐标与图形的性质,熟练掌握平面内点的坐标的特点及勾股定理逆定理、两点间的距离公式是解题的关键.

练习册系列答案
相关题目
10.如果a-b=4,ab=7,那么a2b-ab2的值是( )
| A. | -28 | B. | -11 | C. | 28 | D. | 11 |
14.用一个容量为2GB(1GB=210MB)的便携式优盘存储数码照片,若每张数码照片的文件大小都为16MB,则理论上可以存储的照片数是( )
| A. | 212张 | B. | 28张 | C. | 27张 | D. | 26张 |
 如图所示,两个村庄B,C之间的距离为BC=15km,村庄D与C之间有一条笔直的公路,全长为14km,BD之间拟建一条公路,测算其直线距离约13km,已知从B修一到公路CD的道路造价至少为600000元,请以上述标准计算出若要修建BD之间的公路最低造价是多少元?
如图所示,两个村庄B,C之间的距离为BC=15km,村庄D与C之间有一条笔直的公路,全长为14km,BD之间拟建一条公路,测算其直线距离约13km,已知从B修一到公路CD的道路造价至少为600000元,请以上述标准计算出若要修建BD之间的公路最低造价是多少元?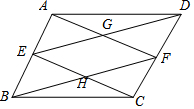 在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.
在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.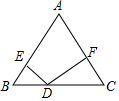 如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.
如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.