题目内容
12．
如图所示，两个村庄B，C之间的距离为BC=15km，村庄D与C之间有一条笔直的公路，全长为14km，BD之间拟建一条公路，测算其直线距离约13km，已知从B修一到公路CD的道路造价至少为600000元，请以上述标准计算出若要修建BD之间的公路最低造价是多少元？
分析 过点B作BE⊥CD于点E，设CE=x，则DE=14-x，再由勾股定理求出x的值，进而可得出BE的长，据此可得出结论．
解答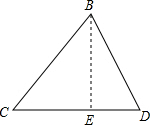 
解：过点B作BE⊥CD于点E，设CE=x，则DE=14-x，
则BC2-CE2=BD2-DE2，
∵BC=15km，CD=14km，BD=13km，
∴152-x2=132-（14-x）2，解得x=9，
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12km．
∵从B修一到公路CD的道路造价至少为600000元，
∴若要修建BD之间的公路最低造价=12×$\frac{600000}{13}$=$\frac{7200000}{13}$（元）．
答：要修建BD之间的公路最低造价是$\frac{7200000}{13}$元．
点评 本题考查的是勾股定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．某酒店有三人间、双人间客房若干，各种房型每天的收费标准如下：
一个30人的旅游团到该酒店入住，选择了一些双人普通间和三人豪华间入住，且恰好住满，己知该旅游团当日住宿费用共计3620元，问该旅游团入住的双人普通间和三人豪华间各为几间？
| 普通（元/间/天） | 豪华（元/间/天） | |
| 三人间 | 240 | 500 |
| 双人间 | 180 | 420 |
20．某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表．A产品为x（件），总利润y（万元）
（1）写出y与x的函数关系式；
（2）如果工厂计划投入资金不多于42万元，如何安排生产才能使获利最大？并求出最大利润．
| A种产品 | B种产品 | |
| 成本（万元/件） | 2 | 5 |
| 利润（万元/件） | 1 | 3 |
（2）如果工厂计划投入资金不多于42万元，如何安排生产才能使获利最大？并求出最大利润．
如图，直线AA1∥BB1∥CC1，若AB=8，BC=4，A1C1=9，线段B1C1长为3．