题目内容
12.阅读理解:对于二次三项式x2+2ax+a2可以直接用公式法分解为(x+a)2的形式,但对于二次三项式x2+2ax-8a2,就不能直接用公式法了.我们可以在二次三项式x2+2ax-8a2中先加上一项a2,使其成为完全平方式,再减去a2这项,使整个式子的值不变,于是又:x2+2ax-8a2
=x2+2ax-8a2+a2-a2
=(x2+2ax+a2)-8a2-a2
=(x+a)2-9a2
=[(x+a)+3a][(x+a)-3]
=(x+4a)(x-2a)
像这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请认真阅读以上的添(拆)项法,并用上述方法将二次三项式:x2+2ax-3a2分解因式.
(2)直接填空:请用上述的添项法将方程的x2-4xy+3y2=0化为(x-y)•(x-3y)=0并直接写出y与x的关系式.(满足xy≠0,且x≠y)
(3)先化简$\frac{x}{y}$-$\frac{y}{x}$-$\frac{{x}^{2}+{y}^{2}}{xy}$,再利用(2)中y与x的关系式求值.
分析 (1)仿照阅读材料中的添(拆)项法,将原式分解即可;
(2)用上述的添项法将方程变形,利用两数相乘积为0,两数中至少有一个为0得到x与y的关系式即可;
(3)原式通分并利用同分母分式的减法法则计算,约分后将x与y的关系式代入计算即可求出值.
解答 解:(1)x2+2ax-3a2=x2+2ax+a2-4a2=(x+a)2-4a2=(x+a+2a)(x+a-2a)=(x+3a)(x-a);
(2)x2-4xy+3y2=x2-4xy+4y2-y2=(x-2y)2-y2=(x-2y+y)(x-2y-y)=(x-y)(x-3y);x=y或x=3y;
故答案为:y;3y
(3)原式=$\frac{{x}^{2}-{y}^{2}-{x}^{2}-{y}^{2}}{xy}$=$\frac{-2{y}^{2}}{xy}$=-$\frac{2y}{x}$,
若x=3y,原式=-$\frac{2}{3}$.
点评 此题考查了因式分解-添(拆)项法,读懂阅读材料运用添(拆)项法是解本题的关键.

练习册系列答案
相关题目
3.若$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{7}$,且a-b+c=12,则2a-3b+c等于( )
| A. | $\frac{3}{7}$ | B. | 2 | C. | 4 | D. | 12 |
7.分式$\frac{x+1}{x-2}$无意义,则x的取值是( )
| A. | x≠2 | B. | x≠-1 | C. | x=2 | D. | x=-1 |
17.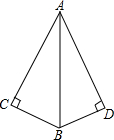 如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.
如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.
以下给出的条件适合的是( )
 如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.
如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
| A. | AC=AD | B. | AB=AB | C. | ∠ABC=∠ABD | D. | ∠BAC=∠BAD |
 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.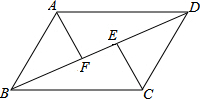 如图,在?ABCD中,点E、F分别是对角线BD上两点,且BF=DE,连接AF、CE.求证:四边形AFCE是平行四边形.
如图,在?ABCD中,点E、F分别是对角线BD上两点,且BF=DE,连接AF、CE.求证:四边形AFCE是平行四边形.