题目内容
4.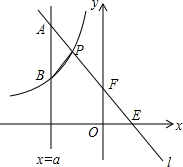 如图,直线y=kx+b与坐标轴分别交于点E、F,与双曲线y=-$\frac{m}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,直线y=kx+b与坐标轴分别交于点E、F,与双曲线y=-$\frac{m}{x}$(x<0)交于点P(-1,4),且F是PE的中点.(1)求双曲线y=-$\frac{m}{x}$和直线y=kx+b的解析式;
(2)若平行于y轴的直线x=a与直线y=kx+b交于点A,与双曲线交于点B(A与B不重合),问a为何值时,PA=PB?
分析 (1)把P代入y=-$\frac{m}{x}$(x<0),根据待定系数法即可求得双曲线的解析式,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为-2a+2,B点的纵坐标为-$\frac{4}{a}$,D点的纵坐标为4,列出方程求解即可.
解答  解:(1)∵y=-$\frac{m}{x}$(x<0)经过点P(-1,4),
解:(1)∵y=-$\frac{m}{x}$(x<0)经过点P(-1,4),
∴4=-$\frac{m}{-1}$
∴m=1×4=4,
∴双曲线为y=-$\frac{4}{x}$,
∵F是PE的中点,
∴OF=$\frac{1}{2}$×4=2,
∴F(0,2),
∴$\left\{\begin{array}{l}{-k+b=4}\\{b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线l的解析式为y=-2x+2;
(2)如图,过P作PD⊥AB,垂足为点D,
∵PA=PB,
∴点D为AB的中点,
又∵由题意知A点的纵坐标为-2a+2,B点的纵坐标为-$\frac{4}{a}$,D点的纵坐标为4,
∴得方程-2a+2-(-$\frac{4}{a}$)=2×4,
解得a1=-2,a2=-1(舍去).
∴当a=-2时,PA=PB.
点评 本题主要考查了反比例函数与一次函数的交点,解题的重点是求出双曲线和直线l的解析式.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
18.已知:a+b=m,计算a2+2ab+b2+1的结果是( )
| A. | (m+1)2 | B. | m2+1 | C. | m2 | D. | m2-1 |
19.下列运算错误的是( )
| A. | a-2•a-1=a2 | B. | (a2)-3=a-6 | ||
| C. | a2÷a-3=a5 | D. | a-n=($\frac{1}{a}$)n(n为正整数) |
14.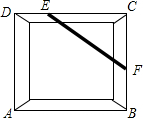 如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
 如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )| A. | 两点之间线段最短 | B. | 矩形的对称性 | ||
| C. | 矩形的四个角都是直角 | D. | 三角形的稳定性 |
 如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积.
如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积. 如图,平行四边形ABCD中,BC=2AB,点M为AD的中点,则∠BMC=90°.
如图,平行四边形ABCD中,BC=2AB,点M为AD的中点,则∠BMC=90°. 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.