题目内容
13．试比较$\sqrt{{a}^{2}}$，$\sqrt{（-a）^{2}}$，-$\sqrt{{a}^{2}}$，说说它们之间有什么关系？分析 首先利用二次根式的意义于性质化简，再进一步比较即可．
解答 解：∵$\sqrt{{a}^{2}}$=|a|，$\sqrt{（-a）^{2}}$=|a|，-$\sqrt{{a}^{2}}$=-|a|，
∴$\sqrt{{a}^{2}}$=$\sqrt{（-a）^{2}}$，
$\sqrt{{a}^{2}}$，$\sqrt{（-a）^{2}}$与-$\sqrt{{a}^{2}}$互为相反数．
点评 此题考查二次根式的性质于化简，掌握二次根式的化简方法是解决问题的关键．
练习册系列答案
相关题目
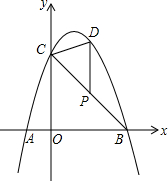抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．
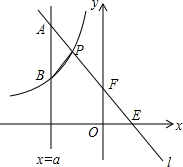如图，直线y=kx+b与坐标轴分别交于点E、F，与双曲线y=-$\frac{m}{x}$（x＜0）交于点P（-1，4），且F是PE的中点．
如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是点N．
8．在△ABC中，a=2，c=$\frac{4\sqrt{3}}{3}$，∠A=60°，则△ABC的面积为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |
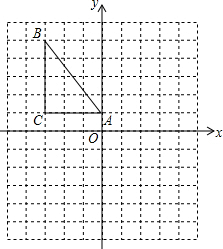如图，已知Rt△ABC中，∠C=90°，AC=3，BC=4，在如图的坐标系中，点A的坐标为（0，1），点B的坐标为（-3，5），AC与x轴平行．
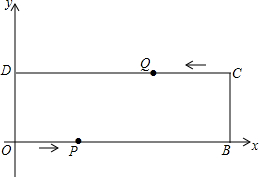已知长方形的生活小区OBCD的边长分别为40米和130米，如图，建立平面直角坐标系，“创文明城市”宣传车点P从点O出发，沿OB运动至点B停止，宣传车点Q从点C出发，沿CD运动至点D停止，两车同时出发，速度都是1米/秒；宣传车音响半径可达25米，（两点间距离公式：|AB|=$\sqrt{（{x}_{A}-{x}_{B}）^{2}+（{y}_{A}-{y}_{B}）^{2}}$）
2．
如图，正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ （x＞0）的图象上，顶点A1、B1分别在x轴、y轴的正半轴上，再在其右侧作正方形P2P3 A2B2，顶点P3在反比例函数y=$\frac{2}{x}$ （x＞0）的图象上，顶点A2在x轴的正半轴上，则点P3的坐标为（ ）
如图，正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ （x＞0）的图象上，顶点A1、B1分别在x轴、y轴的正半轴上，再在其右侧作正方形P2P3 A2B2，顶点P3在反比例函数y=$\frac{2}{x}$ （x＞0）的图象上，顶点A2在x轴的正半轴上，则点P3的坐标为（ ）| A． | （$\sqrt{3}+1$，$\sqrt{3}-1$） | B． | （$\sqrt{5}+1$，$\sqrt{5}-1$） | C． | （$\sqrt{3}-1$，$\sqrt{3}+1$） | D． | （$\sqrt{5}-1$，$\sqrt{5}+1$） |