下列命题是假命题的是( )A．平行四边形的对角线互相平分B．平行四边形的对角相等C．平行四边形是轴对称图形D．平行四边形是中心对称图形题目和参考答案——青夏教育精英家教网—

题目内容

19．下列命题是假命题的是（　　）

	A．	平行四边形的对角线互相平分		B．	平行四边形的对角相等
	C．	平行四边形是轴对称图形		D．	平行四边形是中心对称图形

分析根据平行四边形的对角相等，对角线互相平分可判断出A、B正确；再由平行四边形是中心对称图形可对C、D进行判断．

解答解：A、∵平行四边形的对角线互相平分，∴此命题是真命题；
B、∵平行四边形的对角相等，∴此命题是真命题；
C、∵平行四边形是中心对称图形，不是轴对称图形，∴此命题是假命题；
D、∵平行四边形是中心对称图形，∴此命题是真命题．
故选C．

点评本题考查的是命题与定理，熟知平行四边形的性质是解答此题的关键．

练习册系列答案

10．点M为线段AB的一个三等分点，且AM=6，则线段AB的长为9或18．

7．比较大小：-0.33＞-$\frac{1}{3}$（填“＜”或“＞”）

14．（1）求x的值：4（x+1）²=64
（2）计算：$\sqrt{25}$+2^-2-$\root{3}{27}$-（$\sqrt{3}$-1）⁰．

4．把下列各数填在相应的大括号内：
$\frac{22}{7}$，0，3.14，-$\frac{2}{3}$，-0.55，8，-2．
正数集合：{             …}；
整数集合：{             …}；
分数集合：{             …}．

11．

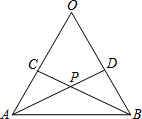如图所示，AO=BO，CO=DO，连接AD、BC，设AD、BC相交于点P．结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．以上结论中（　　）

8．

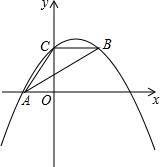如图，抛物线y=ax²+bx+c经过A（-3.0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO．
（1）求抛物线的解析式；
（2）线段AB上有一动点P，过点P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值．

9．下列四组线段中，可以构成直角三角形的是（　　）

试题分类