题目内容
11．
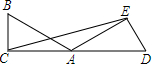如图，已知∠BAC=40°，把△ABC绕着点A顺时针旋转，使得点B与CA的延长线上的点D重合．（1）△ABC旋转了多少度？
（2）连接CE，试判断△AEC的形状．
（3）求∠AEC的度数．
分析 （1）根据题意求出∠BAD的度数，即旋转角的度数，得到答案；
（2）根据旋转变换的性质得到AC=AE，根据等腰三角形的判定定理判断即可；
（3）根据三角形内角和定理和等腰三角形的性质解答即可．
解答 解：（1）∵∠BAC=40°，
∴∠BAD=140°，
∴△ABC旋转了140°；
（2）由旋转的性质可知，AC=AE，
∴△AEC是等腰三角形；
（3）由旋转的性质可知，∠CAE=∠BAD=140°，又AC=AE，
∴∠AEC（180°-140°）÷2=20°．
点评 本题考查的是旋转变换的性质，理解旋转三要素：旋转中心、旋转方向、旋转角度的概念、掌握旋转变换的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
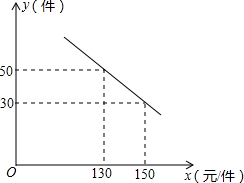网购的普及标志着我国零售业进入了电商时代．某淘宝网店购进一种成本为100元/件的新商品，在试销中发现：销售单价x（元）与每天销售量y（件）之间满足如图所示的关系．
如图，AB是⊙O的直径，E是弧BC的中点，OE交BC于点D，OD=3，DE=2，求BC和AD．
16．如图所示的四个图形中，对称轴为2条的图形有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图所示，直线AB，CD相交于点O，已知∠AOC=80°，OE把∠BOD分成两部分，且∠BOE：∠EOD=2：3，求∠EOD和∠AOE的度数．
如图是一些小正方体所搭几何体的俯视图，小正方形中的数字表示该位置的小正方体的个数，请画出这个几何体的主视图和左视图：