题目内容
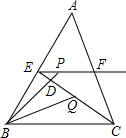 如图,在△ABC中,BC=6
如图,在△ABC中,BC=6| 2 |
| 1 |
| 2 |
| 2 |
考点:相似三角形的判定与性质
专题:
分析:延长BQ交EF于G,容易证得△EQG≌△CQB,得出EG=BC,然后证得三角形PBG是等腰三角形即可.
解答:
解:延长BQ交EF于G,
∵E、F分别是AB、AC的中点,
∴EG∥BC,EF=
BC,
∴∠QBC=∠G,
在△EQG与△CQB中,
,
∴△EQG≌△CQB(AAS)
∴EG=BC=6
,
∵∠PBQ=∠CBQ,∠PGB=∠QBC,
∴∠PBG=∠PGB,
∴PB=PG,
∴BP=PG=EG-EP=BC-EP=6
-
=5
.
故答案为5
.

解:延长BQ交EF于G,
∵E、F分别是AB、AC的中点,
∴EG∥BC,EF=
| 1 |
| 2 |
∴∠QBC=∠G,
在△EQG与△CQB中,
|
∴△EQG≌△CQB(AAS)
∴EG=BC=6
| 2 |
∵∠PBQ=∠CBQ,∠PGB=∠QBC,
∴∠PBG=∠PGB,
∴PB=PG,
∴BP=PG=EG-EP=BC-EP=6
| 2 |
| 2 |
| 2 |
故答案为5
| 2 |
点评:本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,作出辅助线构建等腰三角形是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用科学记数法表示0.0002014,正确的是( )
| A、2.014×104 |
| B、0.2014×10-3 |
| C、2.014×10-4 |
| D、2.014×10-5 |
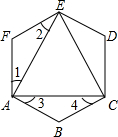 如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.
如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数. 科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表: 如图,在五边形ABCDE中,若∠D=95°,则∠1+∠2+∠3+∠4=
如图,在五边形ABCDE中,若∠D=95°,则∠1+∠2+∠3+∠4=