题目内容
12. 如图,在一块矩形的荒地上修建两条互相垂直且宽度相同的小路,使剩余面积是原矩形面积的一半,具体尺寸如图所示.求小路的宽是多少?设小路的宽是xm,根据题意可列方程为(30-x)(20-x)=$\frac{1}{2}$×30×20.
如图,在一块矩形的荒地上修建两条互相垂直且宽度相同的小路,使剩余面积是原矩形面积的一半,具体尺寸如图所示.求小路的宽是多少?设小路的宽是xm,根据题意可列方程为(30-x)(20-x)=$\frac{1}{2}$×30×20.
分析 把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的种植花草部分是一个长方形,根据长方形的面积公式列方程求解即可.
解答 解:设道路的宽应为x米,由题意有
(30-x)(20-x)=$\frac{1}{2}$×30×20.
故答案为:(30-x)(20-x)=$\frac{1}{2}$×30×20.
点评 此题主要考查了一元二次方程的应用,把中间修建的两条道路分别平移到矩形地面的最上边和最左边是做本题的关键.

练习册系列答案
相关题目
3.圆的周长是2π,如果一条直线与圆心的距离是$\frac{π}{2}$,那么这条直线与这个圆的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
20.部队准备从新兵中组建一个升旗部队,抽查了一批新兵的身高,在这次实验中,部队最关心的是新兵身高数据的( )
| A. | 平均数 | B. | 加权平均数 | C. | 中位数 | D. | 众数 |
7.等腰三角形的底和腰是方程x2-7x+12=0的两个根,则这个三角形的周长是( )
| A. | 11 | B. | 10 | C. | 11或10 | D. | 不能确定 |
17.关于对位似图形的表述,下列命题正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意一组对应点P,P′与位似中心O的距离满足OP=k•OP′.
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意一组对应点P,P′与位似中心O的距离满足OP=k•OP′.
| A. | ①②③④ | B. | ②③④ | C. | ②③ | D. | ②④ |
1.下列多项式能用平方差公式因式分解的是( )
| A. | a2+b2 | B. | -a2-b2 | C. | (-a2)+(-b)2 | D. | (-a)2+(-b)2 |
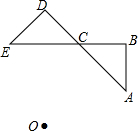 如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.
如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.