题目内容
 如图是矩形ABCD剪去一角所成图形,AB=6cm,BC=8cm,AE=5cm,CF=2cm.一动点P以1cm/s的速度沿折线AE-EF-FC运动,设点P运动的时间为x(s),△ABP的面积为y(cm2),则y与x之间的函数图象大致为( )
如图是矩形ABCD剪去一角所成图形,AB=6cm,BC=8cm,AE=5cm,CF=2cm.一动点P以1cm/s的速度沿折线AE-EF-FC运动,设点P运动的时间为x(s),△ABP的面积为y(cm2),则y与x之间的函数图象大致为( )A、 |
B、 |
C、 |
D、 |
考点:动点问题的函数图象
专题:
分析:分①点P在AE上时,利用三角形的面积公式列式表示出y与x的函数关系;②点P在EF上时,过点P作PH⊥DE于H,先求出DE、DF,再利用勾股定理列式求出EF,然后利用∠DEF的余弦列式求出EH,从而得到点P到AB的距离,然后根据三角形的面积公式列式表示出y与x的函数关系式;③点P在FC上时,点P到AB的距离等于BC的长度,然后利用三角形的面积公式列式求出y,最后根据各选项图形选择即可.
解答: 解:①点P在AE上时,y=
解:①点P在AE上时,y=
AB•x=
×6x=3x(0≤x≤5),
②点P在EF上时,过点P作PH⊥DE于H,
∵AB=6cm,BC=8cm,AE=5cm,CF=2cm,
∴DE=8-5=3cm,DF=6-2=4cm,
由勾股定理得,EF=
=
=5cm,
∴EH=PE•cos∠DEF=(x-5)•
=
,
∴AH=AE+EH=5+
=
x+2,
∴y=
AB•AH=
×6×(
x+2)=
x+6(5<x≤10);
③点P在FC上时,点P到AB的距离等于BC的长度,
所以,y=
AB•BC=
×6×8=24(10<x<12),
纵观各选项,只有D选项图形符合.
故选D.
 解:①点P在AE上时,y=
解:①点P在AE上时,y=| 1 |
| 2 |
| 1 |
| 2 |
②点P在EF上时,过点P作PH⊥DE于H,
∵AB=6cm,BC=8cm,AE=5cm,CF=2cm,
∴DE=8-5=3cm,DF=6-2=4cm,
由勾股定理得,EF=
| DE2+DF2 |
| 32+42 |
∴EH=PE•cos∠DEF=(x-5)•
| 3 |
| 5 |
| 3(x-5) |
| 5 |
∴AH=AE+EH=5+
| 3(x-5) |
| 5 |
| 3 |
| 5 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
③点P在FC上时,点P到AB的距离等于BC的长度,
所以,y=
| 1 |
| 2 |
| 1 |
| 2 |
纵观各选项,只有D选项图形符合.
故选D.
点评:本题考查了动点问题函数图象,主要利用了勾股定理,三角形的面积,锐角三角函数,难点在于根据点P的位置分三段讨论,求出y与x的函数关系式更容易理解.

练习册系列答案
相关题目
直线y=kx-2与x轴的交点是(1,0),则k的值是( )
| A、3 | B、2 | C、-2 | D、-3 |
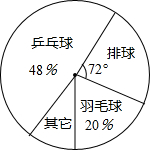 某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法
某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的
| 1 |
| 5 |
③最喜欢羽毛球的学生达到班级学生总数的12人.
④最喜欢其他运动的学生达到12%
其中正确的结论为( )
| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
定义新运算:对任意有理数a、b,都有a⊕b=a2-b,例如:3⊕2=32-2=7,那么2⊕1的值为( )
| A、-2 | B、2 | C、-3 | D、3 |
已知关于x的不等式
有四个整数解,则a的取值范围是( )
|
| A、10<a<11 |
| B、10≤a<11 |
| C、10<a≤11 |
| D、10≤a≤11 |
若x+m与x+
乘积的值不含x项,则m的值为( )
| 1 |
| 4 |
A、
| ||
| B、4 | ||
C、-
| ||
| D、-4 |
在四边形中,能判定这个四边形是正方形的条件是( )
| A、对角线相等,对边平行且相等 |
| B、一组对边平行,一组对角相等 |
| C、对角线互相平分且相等,对角线互相垂直 |
| D、一组邻边相等,对角线互相平分 |