题目内容
 如图,AB为⊙O的直径,DC切⊙O于C,OD交⊙O于E,
如图,AB为⊙O的直径,DC切⊙O于C,OD交⊙O于E, |
| CE |
 |
| BE |
考点:切线的性质
专题:证明题
分析:连接OC,BC,AC,由切线的性质得OC⊥CD,∠D+∠COD=90°,根据直径所对的圆周角等于等于90°,∠CAB+∠B=90°,由同弧所对的圆周角相等,得出∠AEC=∠B,再根据
=
,∠CAB=∠COE,即可得出答案.
 |
| CE |
 |
| BE |
解答: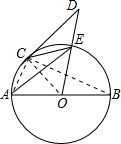 证明:连接OC,BC,AC,
证明:连接OC,BC,AC,
∵DC切⊙O于C,
∴OC⊥CD,
∴∠D+∠COD=90°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵∠AEC=∠B,
∴∠CAB+∠AEC=90°,
∵
=
,
∴∠COE=∠CAB,
∴∠AEC+∠COE=90°,
∴∠AEC=∠D.
 证明:连接OC,BC,AC,
证明:连接OC,BC,AC,∵DC切⊙O于C,
∴OC⊥CD,
∴∠D+∠COD=90°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵∠AEC=∠B,
∴∠CAB+∠AEC=90°,
∵
 |
| CE |
 |
| BE |
∴∠COE=∠CAB,
∴∠AEC+∠COE=90°,
∴∠AEC=∠D.
点评:本题考查了切线的性质,以及直径所对的圆周角等于90°,同弧所对的圆周角的等于圆心角的一半.

练习册系列答案
相关题目
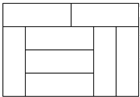 8个一样大小的长方形恰好拼成一个大的长方形(如图),若大长方形的宽为8cm,则每一个小长方形的面积为( )
8个一样大小的长方形恰好拼成一个大的长方形(如图),若大长方形的宽为8cm,则每一个小长方形的面积为( )| A、8cm2 |
| B、12cm2 |
| C、16cm2 |
| D、20cm2 |
 已知平行四边形ABCD的对角线相交于点O,BD=
已知平行四边形ABCD的对角线相交于点O,BD=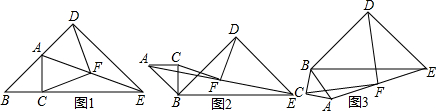
 已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.
已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.