题目内容
在直角坐标系中,由坐标轴和x=5,y=5这四条直线围成的区域(包括边界)中,四个顶点都是整点的正方形个数为 (若x、y为整数,则(x,y)为整点).
考点:坐标与图形性质
专题:
分析:作出图形,然后从边长是1、2、3、4、5考虑求解,然后列式计算即可得解.
解答: 解:如图,边长是1的正方形有52=25个,
解:如图,边长是1的正方形有52=25个,
边长是2的正方形有42=16,
边长是3的正方形有32=9,
边长是4的正方形有22=4,
边长是5的正方形有1个,
所以,正方形共有:25+16+9+4+1=55个.
故答案为:55.
 解:如图,边长是1的正方形有52=25个,
解:如图,边长是1的正方形有52=25个,边长是2的正方形有42=16,
边长是3的正方形有32=9,
边长是4的正方形有22=4,
边长是5的正方形有1个,
所以,正方形共有:25+16+9+4+1=55个.
故答案为:55.
点评:本题考查了坐标与图形性质,从边长的角度考虑求解更简便,作出图形更形象直观.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中,错误的是( )
| A、所有的等边三角形都相似 |
| B、所有的等腰直角三角形都相似 |
| C、所有的矩形都相似 |
| D、所有的正方形都相似 |
比较大小:-3
( )-2
.
| 2 |
| 3 |
| A、> | B、< | C、= | D、不确定 |
 如图,AB为⊙O的直径,DC切⊙O于C,OD交⊙O于E,
如图,AB为⊙O的直径,DC切⊙O于C,OD交⊙O于E,
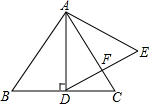 如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.
如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.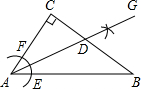 如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图: