题目内容
11. 红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:(1)求出样本容量,并补全直方图;
(2)该年级共有学生600人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有2位女生,E组发言的学生中恰有1位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
分析 (1)求得B组所占的百分比,然后根据B组有10人即可求得总人数,即样本容量,然后求得C组的人数,从而补全直方图;
(2)利用由样本估计总体的方法,即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所抽的两位学生恰好是一男一女的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵B、E两组发言人数的比为5:2,E组发言人数占8%,
∴B组发言的人数占20%,
由直方图可知B组人数为10人,
所以,被抽查的学生人数为:10÷20%=50人,
∴样本容量为50.
F组人数为:50×(1-6%-20%-30%-26%-8%)
=50×(1-90%)
=50×10%,
=5(人),
C组人数为:50×30%=15(人),
E组人数为:50×8%=4人
补全的直方图如图:
(2)估计全年级在这天里发言次数不少于12次的人数:600×(8%+10%)=108(人);
(3)根据题意得:A组共有:50×6%=3(人),有女生1人,则有男生3-1=2(人);E组共有50×8%=4(人),有男生2人,则有女生4-2=2(人);
画树状图得:
∵共有12种等可能的结果,其中所抽的两位学生恰好是一男一女的有6种情况,
∴所抽的两位学生恰好是一男一女的概率为:$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及直方图的知识.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
1.若2 014个有理数的积是0,则( )
| A. | 每个因数都不为0 | B. | 每个因数都为0 | ||
| C. | 最多有一个因数为0 | D. | 至少有一个因数为0 |
19.表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2.
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 x(cm) | 561 | 560 | 561 | 560 |
| 方差s2(cm2) | 35 | 35 | 155 | 165 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
20. 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )| A. | 4对 | B. | 1对 | C. | 2对 | D. | 3对 |
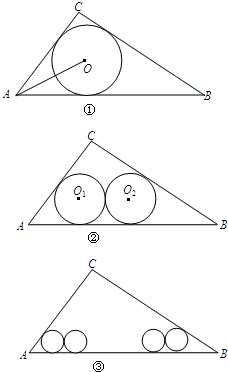 在△ABC中,已知∠C=90°,AC=6,BC=8.
在△ABC中,已知∠C=90°,AC=6,BC=8.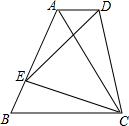 如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.
如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.