题目内容
13.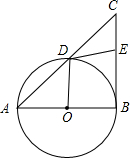 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC的中点,连接DE、OD.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC的中点,连接DE、OD.(1)求证:DE是⊙O的切线;
(2)四边形OBED能否是菱形?如果能,试说明Rt△ABC还应满足什么条件;如果不能,也请说明理由.
分析 (1)欲证明DE是⊙O的切线,只要证明△OED≌△OEB得∠ODE=∠OBE=90°即可.
(2)当AB=BC时,四边形OBED是菱形,根据三角形中位线定理即可证明.
解答 (1)证明:如图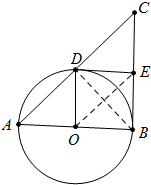 连接BD、OE.
连接BD、OE.
∵AB是直径,
∴∠ADB=90°,
在RT△BCD中,∵∠BDC=90°,EC=EB,
∴DE=EB=EC,
在△OED和△OEB中,
$\left\{\begin{array}{l}{OE=OE}\\{DE=EB}\\{OD=OB}\end{array}\right.$,
∴△OED≌△OEB,
∴∠ODE=∠OBE,
∵∠ABC=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)当AB=BC时,四边形OBED是菱形.
证明:∵AB是直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴AD=DC,∵AO=OB,
∴OD=$\frac{1}{2}$BC,
∴OD=OB=DE=EB,
∴四边形ODEB是菱形.
点评 本题考查切线的判定和性质、菱形的判定、三角形中位线定理、全等三角形的判定和性质等知识,解题的关键是掌握证明切线的方法,利用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
3. 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
4.一组数据2,0,-2,1,3的平均数是( )
| A. | 0.8 | B. | 1 | C. | 1.5 | D. | 2 |
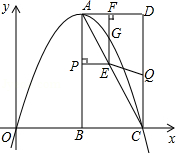 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.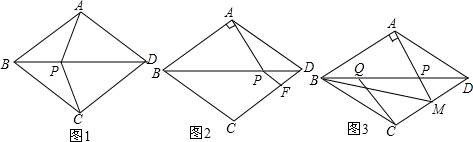 如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,