题目内容
4.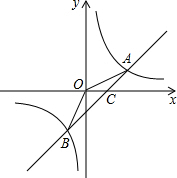 已知反比例函数y=$\frac{k}{2x}$和一次函数y=kx-1交于A、B两点,其中A点坐标为(1,b).
已知反比例函数y=$\frac{k}{2x}$和一次函数y=kx-1交于A、B两点,其中A点坐标为(1,b).(1)求反比例函数和一次函数的解析式;
(2)已知点B的横坐标为-$\frac{1}{2}$,求△AOB的面积;
(3)在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;如不存在,请说明理由.
分析 (1)首先根据题意得出$\frac{k}{2}$=b,k-1=b,进而求得b=1,k=2,从而求得一次函数的解析式;
(2)根据△AOB的面积=S△AOC+S△BOC求解;
(3)分两种情况考虑:①当OA是底边时,则OA的垂直平分线和x轴的交点;②当OA是腰时,则分别以O、A为圆心,以OA为半径画弧,和x轴的交点(点O除外).
解答 解:(1)∵反比例函数y=$\frac{k}{2x}$和一次函数y=kx-1过A(1,b),
∴$\frac{k}{2}$=b,k-1=b,
∴b=1,k=2,
∴反比例函数解析式为y=$\frac{1}{x}$,一次函数的解析式为y=2x-1;
(2)∵点B的横坐标为-$\frac{1}{2}$,
∴点B的纵坐标为-2,
由一次函数的解析式y=2x-1,得直线AB与x轴的交点是C($\frac{1}{2}$,0),
△AOB的面积=S△AOC+S△BOC=$\frac{1}{2}$×$\frac{1}{2}$×1+$\frac{1}{2}$×$\frac{1}{2}$×2=$\frac{3}{4}$.
(3)∵A(1,1),
∴OA=$\sqrt{2}$,
①若OA=OP,
则OP=$\sqrt{2}$,
∴点P的坐标为:($\sqrt{2}$,0)或(-$\sqrt{2}$,0);
②若AO=AP,
过A作AD⊥x轴于D,
∴OD=1,
∴OP=2OD=2,
∴点P的坐标为(2,0);
③若OP=AP,
则P是OA的垂直平分线与x轴的交点,
则点P为(1,0).
∴点P的坐标是(1,0)或($\sqrt{2}$,0)或(-$\sqrt{2}$,0)或(2,0).
点评 此题综合考查了待定系数法求函数解析式的方法、三角形的面积的计算方法以及等腰三角形的判定和性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,在△ABC中,CD⊥AB,垂足为D,∠1=∠B,求证:△ABC为直角三角形.
如图,在△ABC中,CD⊥AB,垂足为D,∠1=∠B,求证:△ABC为直角三角形.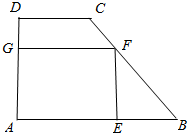 如图,有一块梯形铁板ABCD,AB∥CD,∠A=90°,AB=6cm,CD=2cm,AD=4cm,现在梯形中剪出一内接矩形铁板AEFG,其中E在AB上,F在BC上,G在AD上.若矩形面积为9cm2,则矩形的一边EF长为多少?
如图,有一块梯形铁板ABCD,AB∥CD,∠A=90°,AB=6cm,CD=2cm,AD=4cm,现在梯形中剪出一内接矩形铁板AEFG,其中E在AB上,F在BC上,G在AD上.若矩形面积为9cm2,则矩形的一边EF长为多少?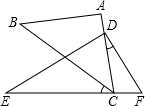 将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.
将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.