题目内容
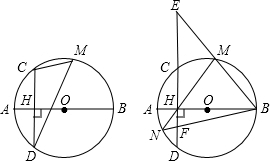
14.如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是$\widehat{CBD}$上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.
分析 (1)在Rt△COH中,利用勾股定理即可解决问题;
(2)只要证明∠CMD=△COA,求出sin∠COA即可;
(3)由△EHM∽△NHF,推出$\frac{HE}{HN}$=$\frac{HM}{HF}$,推出HE•HF=HM•HN,又HM•HN=AH•HB,推出HE•HF=AH•HB,由此即可解决问题.
解答 解:(1)如图1中,连接OC.
∵AB⊥CD,
∴∠CHO=90°,
在Rt△COH中,∵OC=r,OH=r-2,CH=4,
∴r2=42+(r-2)2,
∴r=5.
(2)如图1中,连接OD.
∵AB⊥CD,AB是直径,
∴$\widehat{AD}$=$\widehat{AC}$=$\frac{1}{2}$$\widehat{CD}$,
∴∠AOC=$\frac{1}{2}$∠COD,
∵∠CMD=$\frac{1}{2}$∠COD,
∴∠CMD=∠COA,
∴sin∠CMD=sin∠COA=$\frac{CH}{CO}$=$\frac{4}{5}$.
(3)如图2中,连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF
∴△EHM∽△NHF,
∴$\frac{HE}{HN}$=$\frac{HM}{HF}$,
∴HE•HF=HM•HN,
∵HM•HN=AH•HB,
∴HE•HF=AH•HB=2•(10-2)=16.
点评 本题考查圆综合题、垂径定理、勾股定理、相似三角形的判定和性质、相交弦定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考压轴题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
9.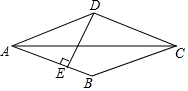 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )| A. | $\frac{75}{13}$ | B. | $\frac{96}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{144}{13}$ |
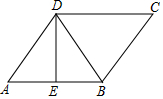 如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.
如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.

 解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.