题目内容
6.如图①,矩形ABCD的四边上分别有E、F、G、H四点,顺次连接四点得到四边形EFGH.若∠1=∠2=∠3=∠4.则四边形EFGH为矩形ABCD的“反射四边形”.
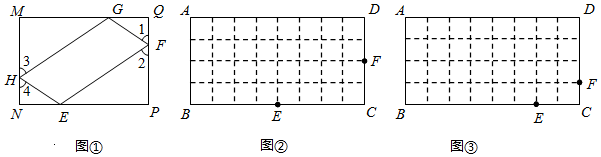
(1)请在图②,图③中画出矩形ABCD的“反射四边形EFGH”.
(2)若AB=4,BC=8.请在图②,③任选其一,计算“反射四边形EFGH”的周长.
分析 (1)根据反射四边形的定义即可得;
(2)利用勾股定理分别求得各边的长度,由周长公式求解可得.
解答 解:(1)如图所示,四边形EFGH即为所求;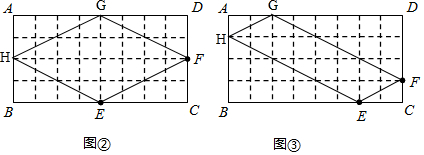
(2)在图②中,EF=FG=GH=HE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴反射四边形EFGH的周长为8$\sqrt{5}$;
在图③中,EF=GH=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,HE=GF=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴反射四边形EFGH的周长为2×$\sqrt{5}$+2×3$\sqrt{5}$=8$\sqrt{5}$.
点评 本题主要考查作图-应用与设计作图,熟练掌握勾股定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.
如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.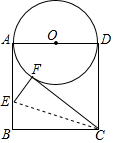 如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.
如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.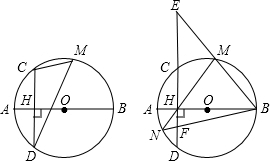
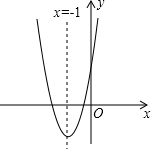 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论: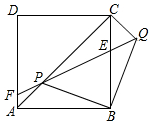 边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.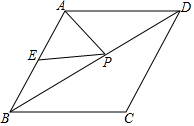 如图,已知菱形ABCD的周长为16,面积为8$\sqrt{3}$,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2$\sqrt{3}$.
如图,已知菱形ABCD的周长为16,面积为8$\sqrt{3}$,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2$\sqrt{3}$.