题目内容
20.k取怎样的整数时,方程组$\left\{\begin{array}{l}{x-2y=8-k}\\{3x+y=4k}\end{array}\right.$的解满足$\left\{\begin{array}{l}{x>0}\\{y<0}\end{array}\right.$.分析 先解出方程组,根据题意列出不等式组,解不等式组得到k的范围,根据整数解的确定方法求解即可.
解答 解:解方程组$\left\{\begin{array}{l}{x-2y=8-k}\\{3x+y=4k}\end{array}\right.$得,
$\left\{\begin{array}{l}{x=\frac{7k+8}{7}}\\{y=\frac{7k-24}{7}}\end{array}\right.$,
$\left\{\begin{array}{l}{\frac{7k+8}{7}>0}\\{\frac{7k-24}{7}<0}\end{array}\right.$,
解得,-$\frac{8}{7}$<k<$\frac{24}{7}$,
因为k为整数,所以k=-1,0,1,2,3.
点评 本题考查的是二元一次方程组的解法、一元一次不等式这组的解法以及整数解的确定,正确解出方程组和不等式组是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
11.下列等式中,计算正确的是( )
| A. | a10÷a9=a | B. | x3•x2=x6 | C. | x3-x2=x | D. | (-3xy)2=6x2y2 |
8. 假如一只小猫走在如图所示的地板上,则它最终停在黑地板上的机会是( )
假如一只小猫走在如图所示的地板上,则它最终停在黑地板上的机会是( )
 假如一只小猫走在如图所示的地板上,则它最终停在黑地板上的机会是( )
假如一只小猫走在如图所示的地板上,则它最终停在黑地板上的机会是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{8}$ |
5. 如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )
如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )
 如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )
如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )| A. | 150° | B. | 60° | C. | 45° | D. | 30° |
10.下列能确定△ABC为等腰三角形的是( )
| A. | ∠A=50°、∠B=80° | B. | ∠A=42°、∠B=48° | ||
| C. | ∠A=2∠B=70° | D. | AB=4、BC=5,周长为15 |
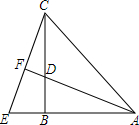 如图,在△ABC中,∠ABC=90°,AB=BC,D是BC上的一点,E是AB延长线上的一点,AD=CE,AD的延长线交CE于点F,则AF与CE垂直吗?为什么?
如图,在△ABC中,∠ABC=90°,AB=BC,D是BC上的一点,E是AB延长线上的一点,AD=CE,AD的延长线交CE于点F,则AF与CE垂直吗?为什么?