题目内容
8.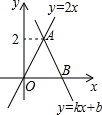 如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )
如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据函数y=2x的图象过点A,求出点A的坐标为(1,2),根据△AOB的面积为2,求出点B的坐标,再分别代入一次函数的解析式求解即可.
解答 解:∵函数y=2x的图象过点A,
∴2=2x,
x=1,
∴点A的坐标为(1,2),
∵△AOB的面积为2,
∴$\frac{1}{2}$OB×2=2,
∴OB=2,
∴点B的坐标为(2,0),
∴$\left\{\begin{array}{l}{2=k+b}\\{0=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
故选:A.
点评 此题考查了一次函数,用到的知识点是一次函数的图象与性质,关键是根据图形求出一次函数的解析式.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
19.甲、乙两个转盘同时转动,甲转动270圈时,乙恰好转了330圈,已知两个转盘每分钟共转200圈,设甲每分钟转x圈,则列方程为( )
| A. | $\frac{270}{200+x}$=$\frac{330}{x}$ | B. | $\frac{270}{200-x}$=$\frac{330}{x}$ | C. | $\frac{270}{x}$=$\frac{330}{200+x}$ | D. | $\frac{270}{x}$=$\frac{330}{200-x}$ |
16.下列各式中一定是二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{x}$ | C. | $\root{3}{27}$ | D. | $\sqrt{{x}^{2}-1}$ |
3.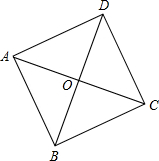 如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
 如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )| A. | AC=BD | B. | AB=BC | C. | ∠ABC=90° | D. | AO=BO |
13.下列说法错误的是( )
| A. | 42的算术平方根为4 | B. | 2的算术平方根为$\sqrt{2}$ | ||
| C. | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D. | $\sqrt{81}$的算术平方根是9 |
20.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | a2•a3=a6 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |