题目内容
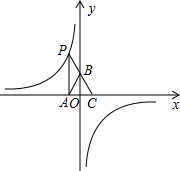 如图,点P是反比例函数y=
如图,点P是反比例函数y=| k |
| x |
| 5 |
| A、0<a<2 | ||||||||
B、
| ||||||||
C、0<a<2或a<
| ||||||||
D、0<a<2或
|
考点:反比例函数综合题
专题:
分析:首先设P(-1,t).根据题意知,A(-1,0),B(0,2),C(1,0),由此易求直线BC的解析式y=-2x+2.把点P的坐标代入直线BC的解析式可以求得点P的坐标,由反比例函数图象上点的坐标特征即可求得k的值;利用分类讨论思想可得:如图①,延长线段BC交抛物线于点M,由图②,当x<a时,∠MBA<∠ABC;作C关于直线AB的对称点C′,连接BC′并延长BC′交双曲线于点M′,当x<a时,∠MBA<∠ABC.
解答:解:如图,作C关于直线AB的对称点C′,连接BC′并延长交双曲线于点M′.
PA垂直x轴于点A(-1,0),
∴OA=1,可设P(-1,t).
又∵AB=
,
∴OB=
=2,
 ∴B(0,2).
∴B(0,2).
又∵点C的坐标为(1,0),
∴直线BC的解析式是:y=-2x+2.
∵点P在直线BC上,
∴t=2+2=4
∴点P的坐标是(-1,4),
∴k=-4,
∴反比例函数的解析式为:y=-
,
①如图1,延长线段BC交双曲线于点M.
由(1)知,直线BC的解析式是y=-2x+2,反比例函数的解析式是y=-
.
则
,
 解得:
解得:
或
(不合题意,舍去).
根据图示知,当0<a<2时,∠MBA<∠ABC;
②∵A(-1,0),B(0,2),
∴直线AB的解析式为:y=2x+2.
直线CC′是与直线AB垂直的,
∵设CC′解析式为:y=-
x+b,
∵C(1,0),
∴b=
,
∴CC′解析式为:y=-
x+
,
∵AC=AC′=2,
∴设C′点横坐标为:x,则纵坐标为:-
x+
,
∴(-x-AO)2+(-
x+
)2=(AC′)2,
解得:x1=-
,x2=1(不合题意舍去),
∴C′(-
,
),则易求直线BC′的解析式为:y=
x+2,
∴
,
解得:x1=
,x2=
,
则根据图示知,当
<a<
时,∠MBA<∠ABC.
综合①②知,当0<a<2或
<a<
时,∠MBA<∠ABC.
故选D.
PA垂直x轴于点A(-1,0),
∴OA=1,可设P(-1,t).
又∵AB=
| 5 |
∴OB=
| AB2-OA2 |
 ∴B(0,2).
∴B(0,2).又∵点C的坐标为(1,0),
∴直线BC的解析式是:y=-2x+2.
∵点P在直线BC上,
∴t=2+2=4
∴点P的坐标是(-1,4),
∴k=-4,
∴反比例函数的解析式为:y=-
| 4 |
| x |
①如图1,延长线段BC交双曲线于点M.
由(1)知,直线BC的解析式是y=-2x+2,反比例函数的解析式是y=-
| 4 |
| x |
则
|
 解得:
解得:
|
|
根据图示知,当0<a<2时,∠MBA<∠ABC;
②∵A(-1,0),B(0,2),
∴直线AB的解析式为:y=2x+2.
直线CC′是与直线AB垂直的,
∵设CC′解析式为:y=-
| 1 |
| 2 |
∵C(1,0),
∴b=
| 1 |
| 2 |
∴CC′解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=AC′=2,
∴设C′点横坐标为:x,则纵坐标为:-
| 1 |
| 2 |
| 1 |
| 2 |
∴(-x-AO)2+(-
| 1 |
| 2 |
| 1 |
| 2 |
解得:x1=-
| 11 |
| 5 |
∴C′(-
| 11 |
| 5 |
| 8 |
| 5 |
| 2 |
| 11 |
∴
|
解得:x1=
-11-
| ||
| 2 |
-11+
| ||
| 2 |
则根据图示知,当
-11-
| ||
| 2 |
-11+
| ||
| 2 |
综合①②知,当0<a<2或
-11-
| ||
| 2 |
-11+
| ||
| 2 |
故选D.
点评:本题综合考查了待定系数法求一次函数的解析式,反比例函数图象上点的坐标特征以及分式方程组的解法.解题时,一定要分类讨论,以防漏解.另外,解题的过程中,利用了“数形结合”的数学思想.

练习册系列答案
相关题目
 如图,下列判断正确的是( )
如图,下列判断正确的是( )| A、∠2与∠4是同位角 |
| B、∠2与∠5是对顶角 |
| C、∠3与∠6是同位角 |
| D、∠5与∠3是内错角 |
点(6,-8)是直角坐标系中的一点,O为坐标原点,则OA的长度为( )
| A、6 | B、8 | C、10 | D、12 |
已知a,b,c是实数,且a>b>c,则下列选项正确的是( )
| A、a+b>b+c | ||||
| B、a-b>b-c | ||||
| C、ab>bc | ||||
D、
|
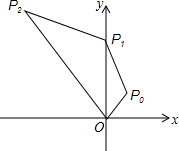 如图,在直角坐标系中,点P0的坐标为(
如图,在直角坐标系中,点P0的坐标为(


