题目内容
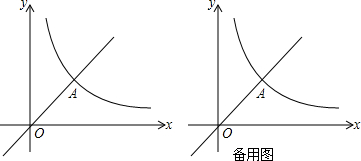
17. 如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是y=-$\sqrt{3}$x2+2$\sqrt{3}$x和y=$\sqrt{3}$x2+2$\sqrt{3}$x(答案不唯一).
如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是y=-$\sqrt{3}$x2+2$\sqrt{3}$x和y=$\sqrt{3}$x2+2$\sqrt{3}$x(答案不唯一).
分析 连接AB,根据姐妹抛物线的二次项的系数互为相反数,一次项系数相等且不等于零,常数项都是零,设抛物线C1的解析式为y=ax2+bx,
根据四边形ANBM恰好是矩形可得△AOM是等边三角形,设OM=2,则点A的坐标是(1,$\sqrt{3}$),求出抛物线C1的解析式,从而求出抛物线C2的解析式.
解答 解:连接AB,
根据姐妹抛物线的定义,可得姐妹抛物线的二次项的系数互为相反数,一次项系数相等且不等于零,常数项都是零,
设抛物线C1的解析式为y=ax2+bx,
根据四边形ANBM恰好是矩形可得:OA=OM,
∵OA=MA,
∴△AOM是等边三角形,
设OM=2,则点A的坐标是(1,$\sqrt{3}$),
则$\left\{\begin{array}{l}{\sqrt{3}=a+b}\\{0=4a+2b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$
则抛物线C1的解析式为y=-$\sqrt{3}$x2+2$\sqrt{3}$x,
抛物线C2的解析式为y=$\sqrt{3}$x2+2$\sqrt{3}$x,
故答案为:y=-$\sqrt{3}$x2+2$\sqrt{3}$x,y=$\sqrt{3}$x2+2$\sqrt{3}$x(答案不唯一).
点评 此题考查了二次函数的图象与几何变换,用到的知识点是姐妹抛物线的定义、二次函数的图象与性质、矩形的判定,关键是根据姐妹抛物线的定义得出姐妹抛物线的二次项的系数、一次项系数、常数项之间的关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.在如图的△ABC中,正确画出AC边上的高的图形是( )
| A. |  | B. |  | C. |  | D. |  |
7.单项式7ab2c2的次数是( )
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
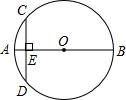 如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为$\frac{5}{2}$.
如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为$\frac{5}{2}$.

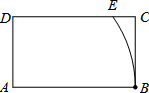 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$.
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$.