题目内容
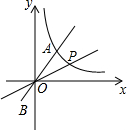 如图,正比例函数y=
如图,正比例函数y=| 3 |
| ||
| x |
A、y=
| ||||
B、y=3
| ||||
| C、y=3x | ||||
D、y=
|
考点:反比例函数与一次函数的交点问题
专题:
分析:作PB⊥x轴于B,AC⊥x轴于C,根据A点坐标可得到∠AOC=60°,由于点P到x轴和正比例函数图象的距离相等,根据角平分线的性质得到∠POB=30°,设P点坐标(a,b),则a=
b,即P点坐标为(
b,b),设直线OP的解析式为y=mx,待定系数法即可求得.
| 3 |
| 3 |
解答:解: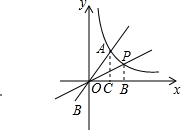 作PB⊥x轴于B,AC⊥x轴于C,如图,
作PB⊥x轴于B,AC⊥x轴于C,如图,
解
得
∵A点坐标为(1,
),即AC=
,OC=1,
∴tan∠AOC=
,
∴∠AOC=60°,
∵点P到x轴和正比例函数图象的距离相等,
∴∠POB=30°,
设P点坐标(a,b),则a=
b,即P点坐标为(
b,b),
设直线OP的解析式为y=mx,
把(
b,b)代入得b=
b•m,
∴m=
,
∴直线OP的解析式为y=
x.
故选A.
 作PB⊥x轴于B,AC⊥x轴于C,如图,
作PB⊥x轴于B,AC⊥x轴于C,如图,解
|
|
∵A点坐标为(1,
| 3 |
| 3 |
∴tan∠AOC=
| 3 |
∴∠AOC=60°,
∵点P到x轴和正比例函数图象的距离相等,
∴∠POB=30°,
设P点坐标(a,b),则a=
| 3 |
| 3 |
设直线OP的解析式为y=mx,
把(
| 3 |
| 3 |
∴m=
| ||
| 3 |
∴直线OP的解析式为y=
| ||
| 3 |
故选A.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及角平分线的性质.

练习册系列答案
相关题目
下列事件,概率为1的是( )
| A、晚上睡觉,当第一次醒来睁开眼睛时,发现天亮了 |
| B、某同学平时每次测试的成绩均低于200分,但今年他的中考成绩却高于700分 |
| C、瓮安三中九年级某班的56名学生中,有31名是女生,从中随机地抽出26名学生组成一个小合唱团,被抽出的26名学生中至少有一名是女生 |
| D、今年“神九”与“天宫一号”成功交汇对接 |
下面等式正确的是( )
| A、-(-5)=-5 |
| B、-|-3|=3 |
| C、|x|=x |
| D、绝对值等于2的数是2和-2 |
在下列图形中,既是中心对称图形,又是轴对称图形,且对称轴只有两条的是( )
| A、圆 | B、平行四边形 |
| C、等边三角形 | D、正方形 |
袋中共有3个红球,3个白球,它们只有颜色上的区别,随机地摸一个后不放回,再随机摸一个,则第一次摸到红球,并且第二次摸到白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
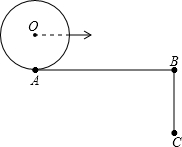 如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动点C时停止,则在此运动过程中,圆心O运动的总路程为
如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动点C时停止,则在此运动过程中,圆心O运动的总路程为 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD.
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD. 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF.