题目内容
如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△ABC≌△BAD．考点：全等三角形的判定
专题：证明题
分析：由垂直的定义可得到∠C=∠D，结合条件和公共边，可证得结论．
解答：证明：∵AC⊥BC，BD⊥AD，
∴∠C=∠D=90，
在Rt△ACB和Rt△BDA中，
，
∴△ACB≌△BDA（HL）．
∴∠C=∠D=90，
在Rt△ACB和Rt△BDA中，
|
∴△ACB≌△BDA（HL）．
点评：本题主要考查全等三角形的判定，掌握全等三角形的判定方法是解题的关键，即SSS、SAS、ASA、AAS和HL．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知点A（-3，2）与点B（x，y）在同一条平行y轴的直线上，且B点到x轴的矩离等于3，则B点的坐标是（ ）
| A、（-3，3） |
| B、（3，-3） |
| C、（-3，3）或（-3，-3） |
| D、（-3，3）或（3，-3） |
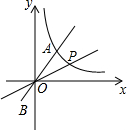如图，正比例函数y=| 3 |
| ||
| x |
A、y=
| ||||
B、y=3
| ||||
| C、y=3x | ||||
D、y=
|
下列图形中，是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
下列各式中结果为负数的是（ ）
| A、-（-3） | ||
| B、（-3）2 | ||
| C、-|-3| | ||
D、
|