题目内容
在实数范围内定义新运算：a△b=a•b-b+1，则不等式3△x≤3的非负整数解为（ ）
| A、-1，0 | B、1 | C、0 | D、0，1 |
考点：一元一次不等式的整数解
专题：新定义
分析：首先根据规定运算，将不等式3△x≤3转化为一元一次不等式，再利用不等式的基本性质解不等式，然后从不等式的解集中找出适合条件的非负整数即可．
解答：解：根据规定运算，不等式3△x≤3可化为3x-x+1≤3，
解得x≤1，
故不等式3△x≤3的非负整数解为0，1．
故选D．
解得x≤1，
故不等式3△x≤3的非负整数解为0，1．
故选D．
点评：本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．
解不等式要依据不等式的基本性质：
（1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；
（2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；
（3）不等式的两边同时乘以或除以同一个负数不等号的方向改变．
解不等式要依据不等式的基本性质：
（1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；
（2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；
（3）不等式的两边同时乘以或除以同一个负数不等号的方向改变．
练习册系列答案
相关题目
如图，AO⊥OB，垂足为O，OC平分∠AOB，则∠AOC的度数为（ ）| A、30° | B、40° |
| C、45° | D、90° |
如图，分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图，则组成这个几何体的小正方体的最多个数是（ ）| A、9个 | B、8个 | C、7个 | D、6 |
如图，在正方形ABCD中，点E、F、G、H均在其内部，且DE=EF=FG=GH=HB=2，∠E=∠F=∠G=∠H=60°，则正方形ABCD的边长为（ ）
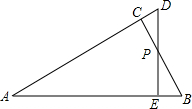把两个一样的直角三角板的30°角重合，其两对边交于点P（如图），连接BD，下列说法错误的是（ ）| A、整个图形是轴对称图形 |
| B、△PEB周长大于DB |
| C、有4对全等三角形（不添线） |
| D、∠EDB=15° |
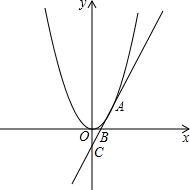已知直线y1=2x-1分别交x轴、y轴于B、C，抛物线y2=mx2过直线y1=2x-1上点A（1，n）．
如图，已知O为直线AC上一点，OB为射线，OM、ON分别是∠AOB、∠COB的平分线，求∠MON的度数．