题目内容
4.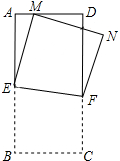 如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).
如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).
分析 连接BM交EF于点G,过点F作FK⊥AB于点K,交BM于点O,根据等腰三角形的性质得到∠FGO=90°,由矩形的性质得到KF=BC=AD,FC=KB,根据余角的性质得到∠KBO=∠OFG,推出△ABM∽△KFE,得到$\frac{AM}{EK}=\frac{AB}{FK}$,由于EK=EF•cosα,即可得到结论.
解答 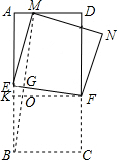 解:连接BM交EF于点G,过点F作FK⊥AB于点K,交BM于点O,
解:连接BM交EF于点G,过点F作FK⊥AB于点K,交BM于点O,
∵EM=EB,∠MEF=∠BEF,
∴EF⊥MB,
即∠FGO=90°,
∵四边形FKBC是矩形,
∴KF=BC=AD,FC=KB,
∵∠FKB=90°,
∴∠KBO+∠KOB=90°,
∵∠GOF+∠GFO=90°,∠GOF=∠KOB,
∴∠KBO=∠OFG,
∵∠A=∠EKF=90°,
∴△ABM∽△KFE,
∴$\frac{AM}{EK}=\frac{AB}{FK}$,
∵EK=EF•cosα,
∴$\frac{AM}{EF•cosα}$=$\frac{AB}{AD}$=$\frac{1}{m}$,
∴$\frac{AM}{EF}$=$\frac{cosα}{m}$.
点评 此题考查了相似三角形的判定与性质、折叠的性质、矩形的性质以及等腰三角形的判定与性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
15.某商品按进价的100%加价出售,经过一段时间,商家为减少库存,决定以7折销售,这时每件商品( )
| A. | 赚40% | B. | 赔30% | C. | 赔40% | D. | 不赔不赚 |
13.已知x-$\frac{1}{x}$=4,则x2+$\frac{1}{{x}^{2}}$的值为( )
| A. | 6 | B. | 16 | C. | 14 | D. | 18 |
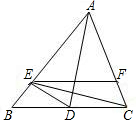 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).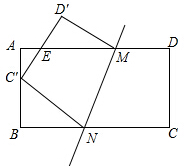 如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.
如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.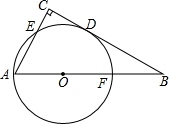 如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.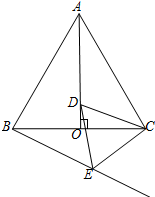 如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.
如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.