题目内容
15.如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
分析 (1)由平行线的性质知∠O=180°-∠B=80°,结合∠A=100°得∠A+∠O=180°,即可得证;
(2)由角平分线的性质可得;
(3)由BC∥OA知∠OCB=∠AOC,结合∠FOC=∠AOC知∠FOC=∠OCB,从而得∠OFB=2∠OCB;
解答 解:(1)∵BC∥OA,
∴∠B+∠O=180°,
∴∠O=180°-∠B=80°,
而∠A=100°,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵OE平分∠BOF,
∴∠BOE=∠FOE=$\frac{1}{2}$∠BOF,
而∠FOC=∠AOC=$\frac{1}{2}$∠AOF,
∴∠EOC=∠EOF+∠COF=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×80°=40°;
(3)不改变,
∵BC∥OA,
∴∠OCB=∠AOC,
∵∠FOC=∠AOC,
∴∠FOC=∠OCB,
∴∠OFB=∠FOC+∠OCB=2∠OCB,即∠OCB:∠OFB的值为1:2.
点评 本题主要考查角平分线的性质和平行线的判定与性质及三角形外角性质,熟练掌握角平分线的性质和平行线的判定与性质是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
5.已知一个等腰三角形一边长为4cm,另一边长为6cm,那么这个等腰三角形的周长为( )
| A. | 14cm | B. | 16cm | C. | 14cm或16cm | D. | 以上都不对 |
6.计算$\frac{1}{3}$a2•(-6ab)的结果正确的是( )
| A. | -2a2b | B. | 2a2b | C. | -2a3b | D. | 2a3b |
5.△ABC的三边分别为下列各组值,其中不是直角三角形三边的是( )
| A. | a=13,b=12,c=5 | B. | a=1.2,b=1.6,c=2 | C. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | D. | a=$\frac{4}{3}$,b=$\frac{5}{3}$,c=1 |
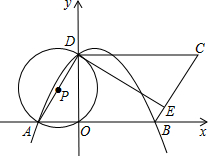 如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.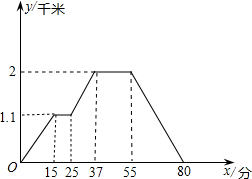 下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:
下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题: