题目内容
15.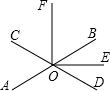 如图,直线AB与CD相交于一点O,OE平分∠BOD,OF⊥OE于点O,∠AOC=62°,则∠COF的度数为59°.
如图,直线AB与CD相交于一点O,OE平分∠BOD,OF⊥OE于点O,∠AOC=62°,则∠COF的度数为59°.
分析 先利用对顶角的性质得到∠BOD=∠AOC=62°,再根据角平分线定义得到∠BOE=$\frac{1}{2}$∠BOD=31°,接着利用垂直定义得到∠EOF=90°,则利用互余得到∠BOF=59°,利用互补得到∠BOC=118°,然后计算∠BOC-∠BOF即可.
解答 解:∵直线AB与CD相交于一点O,
∴∠BOD=∠AOC=62°,
∵OE平分∠BOD,
∴∠BOE=$\frac{1}{2}$∠BOD=31°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°-31°=59°,
∵∠BOC=180°-∠AOC=118°,
∴∠COF=118°-59°=59°.
故答案为59°.
点评 本题考查了垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直.也考查了角平分线的定义和邻补角.

练习册系列答案
相关题目
10.直线l外一点P与直线l上三点的连线段长分别为3cm,4cm,5cm,则点P到直线l的距离( )
| A. | 等于3cm | B. | 等于4cm | C. | 不超过3cm | D. | 大于5cm |
20.某城市自来水费实行阶梯水费,收费标准如下表:
(1)某用户十二月份用水30吨,用含a的代数式表示该用户十二月份所交的水费;
(2)若a=1.5元,某用户十二月份交了30元水费,求该用户十二月份的用水量.
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过20吨的部分 | 超过20吨的部分 |
| 收费标准(元/吨) | a | a+1 | 4 |
(2)若a=1.5元,某用户十二月份交了30元水费,求该用户十二月份的用水量.
4.数轴上-$\frac{1}{2}$表示的点到原点的距离是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |