题目内容
【题目】如图,以正五边形![]() 的顶点
的顶点![]() 为圆心,
为圆心,![]() 为半径作圆弧交
为半径作圆弧交![]() 的延长线于点
的延长线于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交
为半径作圆弧交![]() 的延长线于
的延长线于![]() ,依次进行……得到螺旋线,再顺次连结
,依次进行……得到螺旋线,再顺次连结![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到5块阴影区域,若记它们的面积分别为
,得到5块阴影区域,若记它们的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由题意得,五个扇形的圆心角相等,所以面积比是半径比的平方,根据面积比可表示出五个扇形面积,再根据底相等的三角形面积比等于高的比求出五个三角形的面积比并表示出来,从而分别求出各个阴影部分的面积,再根据![]() 即可求解.
即可求解.
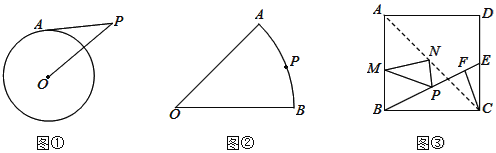
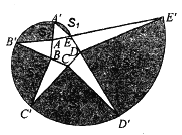
解:因为扇形AEA′、扇形BB′A′、扇形CC′B′、扇形DD′C′、扇形EE′D′圆心角相等,都是72°,半径分别是正五边形半径、半径的二倍、三倍、四倍、五倍,
由扇形面积公式可得,五个扇形面积从小到大的比是1:4:9:16:25,设:扇形AEA′的面积=m,则扇形BB′A′、扇形CC′B′、扇形DD′C′、扇形EE′D′的面积依次为:4m、9m、16m、25m;△AEA′、△BB′A′、△CC′B′、△DD′C′、△EE′D′中,AE=AB=BC=CD=DE,AA′:BB′:CC′:DD′:EE′=1:2:3:4:5,五个三角形分别以AE、AB、BC、CD、DE为底,易证五个三角形的面积比依次为:1:2:3:4:5,设S△AEA′=n,
则S△BB′A′=2n、S△CC′B′=3n、S△DD′C′=4n、S△EE′D′=5n,所以S5=25m-5n , S2=4m-2n , S4=16m-4n , S3=9m-3n , 因为![]() ,所以(25m-5n)-(4m-2n)=1,解得:7m-n=
,所以(25m-5n)-(4m-2n)=1,解得:7m-n=![]() ,所以
,所以![]() =(16m-4n)-(9m-3n)=7m-n=
=(16m-4n)-(9m-3n)=7m-n=![]() .
.
故选:D.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
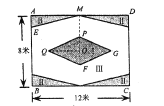
世纪百通优练测系列答案【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,