��Ŀ����
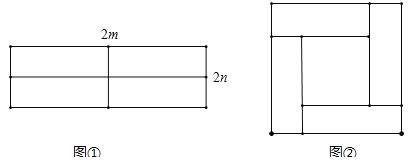
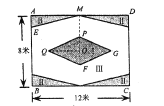
����Ŀ����ͼ��ijУ������12�ף���8�ľ���![]() ���ڳ��ؽ��е���װ�Σ��ֽ��仮��Ϊ������������
���ڳ��ؽ��е���װ�Σ��ֽ��仮��Ϊ������������![]() ������������4��ȫ�ȵ�ֱ�������Σ���ʣ��հײ��ּ�Ϊ����������
������������4��ȫ�ȵ�ֱ�������Σ���ʣ��հײ��ּ�Ϊ����������![]() Ϊ���κ����εĶԳ����ģ�
Ϊ���κ����εĶԳ����ģ�![]() ��
��![]() ��
��![]() ��Ϊ�����ۣ�Ҫ�����������������������
��Ϊ�����ۣ�Ҫ�����������������������![]() �����
�����![]() ������
������![]() ��.
��.
�� | �� | �� | |
���ۣ�Ԫ/��2�� |
|
|
|
��1����![]() ʱ���������������.
ʱ���������������.
��2���ƻ��������������ֱ�����ף������ͬ����ɫ��ש����������������ɫ��ש��
������ͬ���������£��������ڰ�ɫ��������Խ�����ڹ�������Խ��.��![]() Ϊ����ʱ�����ڹ���������ã������ʱ��ɫ��������.
Ϊ����ʱ�����ڹ���������ã������ʱ��ɫ��������.
�����ִ�ש�ĵ����б����£�![]() ��Ϊ������������
��Ϊ������������![]() ��ʱ�����������ש���ܷ������٣������ٷ���Ϊ7200Ԫ����ʱ
��ʱ�����������ש���ܷ������٣������ٷ���Ϊ7200Ԫ����ʱ![]() __________��
__________��
���𰸡���1��8m2;��2��68m2;(3) 40��8
��������
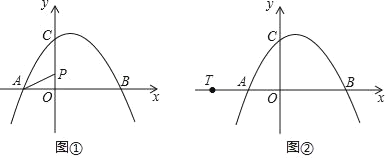
��1���������ĶԳ�ͼ�����ʺ�,![]() ,
,![]() ,
,![]() �ɵ�
�ɵ�![]() ,���ɽ
,���ɽ![]() ʱ��4��ȫ��ֱ�������ε������
ʱ��4��ȫ��ֱ�������ε������
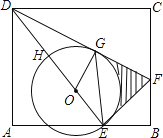
��2����ɫ����������Ǿ��������ȥһ�����ֵ�������ֱ��ú�x�Ĵ���ʽ��ʾ�����κ��ĸ�ȫ��ֱ�������ε�������г�����x�Ľ���ʽ��ʾ��ɫ��������������ɶ���ʽ������![]() ��
��![]() ��
��![]() ������Ա�����ȡֵ��Χ���ٸ��ݶ��κ����������Լ��ɽ��
������Ա�����ȡֵ��Χ���ٸ��ݶ��κ����������Լ��ɽ��
��3�������x=2ʱ����������Լ��ú�m��n�Ĵ���ʽ��ʾ�����ã���Ϊm,n��Ϊ�����������m=40��n=8.
��1�� ��![]() Ϊ�����κ����εĶԳ����ģ�
Ϊ�����κ����εĶԳ����ģ�![]() ����
����![]()
��![]() ��
��![]() ����
����![]()
�൱![]() ʱ��
ʱ��![]() ��
��![]()
��2����![]() ��
��![]()
��![]() -
- ��
��
��![]() ��
��![]() ��
��![]()
��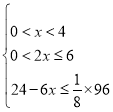 �ⲻ��ʽ���
�ⲻ��ʽ���![]() ��
��
��![]() �����ͼ��
�����ͼ��![]() ʱ��
ʱ��![]() ��
��![]() ���������С.
���������С.
�൱![]() ʱ��
ʱ�� ![]() ȡ�����ֵΪ
ȡ�����ֵΪ![]()
��3���ߵ�![]() ʱ��S��=4x2=16 m2��
ʱ��S��=4x2=16 m2��![]() =12 m2��
=12 m2��![]() =68m2���ܷ���:16��2m+12��5n+68��2m=7200,����ã�5n+14m=600,��Ϊm,n��Ϊ�����������m=40��n=8.
=68m2���ܷ���:16��2m+12��5n+68��2m=7200,����ã�5n+14m=600,��Ϊm,n��Ϊ�����������m=40��n=8.