Question

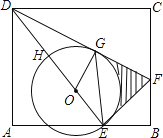
【题目】在菱形ABCD中，E是对角线AC上的一个动点，连结BE并延长交直线AD于点F．

(1)若AB＝10，sin∠BAC＝；

①求对角线AC的长；

②若BE＝4，求AE的长；

(2)若点F在边AD上，且＝k，△BEC和四边形ECDF的面积分别是S1和S2，求的最大值．

Answer 1

【答案】(1)①AC=12；②AE′=8；(2)的最大值为．

【解析】

(1)①连接BD，根据菱形的性质得到AO＝OC，AC⊥BD，根据正弦的定义、勾股定理计算，得到答案；

②分点F在边AD上、点F在边AD的延长线上两种情况，根据勾股定理计算；

(2)连接DE，证明△BCE≌△DCE，设△BCE的面积为S，根据相似三角形的性质求出S△AEF、S△EFD，根据二次函数的性质计算即可．

解：(1)①如图1，连接BD，

∵四边形ABCD是菱形，

∴AO＝OC，AC⊥BD，

在Rr△AOB中，sin∠BAC＝，即，

解得，OB＝8，

由勾股定理得，AO＝＝6，

则AC＝2OA＝12；

②当点F在边AD上时，OE＝＝4，

则AE＝OA﹣OE＝2，

当点F′在边AD的延长线上时，AE′＝OA+OE′＝8；

(2)如图2，连接DE，

∵四边形ABCD是菱形，

∴CB＝CD，∠ACB＝∠ACD，

在△BCE和△DCE中，

，

∴△BCE≌△DCE(SAS)

设△BCE的面积为S，则△DCE的面积为S，

∵AF∥BC，

∴△AEF∽△CEB，

∴＝k2，即S△AEF＝k2S，

∵＝k，

∴，

∴，

解得，S△EFD＝kS﹣k2S，

＝＝﹣k2+k+1＝﹣(k﹣)2+，

当k＝时，的最大值为．