题目内容
如图1,在平面直角坐标系中,A(0,4),B(4,0).
(1)BD平分∠ABO的外角,∠ADO=45°,求∠BAD的大小;
(2)在图1中,求
的值;
(3)如图2,点P在OB上,AP⊥PF,∠OBF=135°,问
是否变化?

(1)BD平分∠ABO的外角,∠ADO=45°,求∠BAD的大小;
(2)在图1中,求
| AE |
| OB |
(3)如图2,点P在OB上,AP⊥PF,∠OBF=135°,问
| AP |
| PF |

考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)由条件可知A、B、O、D四点共圆,再结合角平分线的性质可求得∠BAD;
(2)由条件可证明∠AOD=∠AEO,所以可得AE=OB,可求得比值为1;
(3)由条件可证明Rt△AEP∽Rt△FEB,进一步可证明△AEF∽△PEB,得到△APF为等腰三角形,则可得比值不变.
(2)由条件可证明∠AOD=∠AEO,所以可得AE=OB,可求得比值为1;
(3)由条件可证明Rt△AEP∽Rt△FEB,进一步可证明△AEF∽△PEB,得到△APF为等腰三角形,则可得比值不变.
解答:解:(1)∵OA=OB,∠O=90°,
∴∠OAB=∠OBA=45°,
∵∠ABO=∠ADO=45°,
∴A、O、B、D四点共圆,
∴∠ODB=∠OAB=45°,
∴∠ADB=90°,
∵BD平分∠ABX,∴∠ABD=
(180°-45°)=67.5°,
∴∠BAD=90°-∠ABD=22.5°;
(2)∵∠DAO=45°+22.5°=67.5°,∠ADO=45°,
∴∠AOD=67.5°,
又由△AOE内角和为180°得,∠AEO=180°-∠OAB-∠DOA=67.5°,
∴AE=OA=OB,
∴
=1;
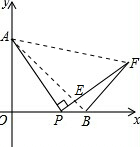 (3)连接AB,交PF于点E,连接AF,
(3)连接AB,交PF于点E,连接AF,
∵OA=OB,
∴∠ABO=45°,
∴∠ABF=135°-45°=90°,
∵∠AEP=∠FEB,
∴Rt△AEP∽Rt△FEB,
∴
=
,
∵∠AEF=∠PEB,
∴△AEF∽△PEB,
∴∠AFE=∠PBE=45°,
∴△APF为等腰三角形,
∴
=1,
即
不变.
∴∠OAB=∠OBA=45°,
∵∠ABO=∠ADO=45°,
∴A、O、B、D四点共圆,
∴∠ODB=∠OAB=45°,
∴∠ADB=90°,
∵BD平分∠ABX,∴∠ABD=
| 1 |
| 2 |
∴∠BAD=90°-∠ABD=22.5°;
(2)∵∠DAO=45°+22.5°=67.5°,∠ADO=45°,
∴∠AOD=67.5°,
又由△AOE内角和为180°得,∠AEO=180°-∠OAB-∠DOA=67.5°,
∴AE=OA=OB,
∴
| AE |
| OB |
 (3)连接AB,交PF于点E,连接AF,
(3)连接AB,交PF于点E,连接AF,∵OA=OB,
∴∠ABO=45°,
∴∠ABF=135°-45°=90°,
∵∠AEP=∠FEB,
∴Rt△AEP∽Rt△FEB,
∴
| AE |
| PE |
| EF |
| BE |
∵∠AEF=∠PEB,
∴△AEF∽△PEB,
∴∠AFE=∠PBE=45°,
∴△APF为等腰三角形,
∴
| AP |
| PF |
即
| AP |
| PF |
点评:本题主要考查相似三角形的判定和性质,掌握复杂图形中寻找三角形相似的条件是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
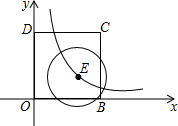 如图,平面直角坐标系中,边长为2正方形OBCD的顶点B在x轴正半轴上,点D在y轴正半轴上,半径为1的⊙E的圆心E在双曲线y=
如图,平面直角坐标系中,边长为2正方形OBCD的顶点B在x轴正半轴上,点D在y轴正半轴上,半径为1的⊙E的圆心E在双曲线y=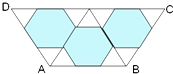 角进行清扫,改成一个小花坛,该等腰梯形上底角为60°,上底是下底的2倍,AB=6m,若按图案在三个正六边形中种上花圃.求:
角进行清扫,改成一个小花坛,该等腰梯形上底角为60°,上底是下底的2倍,AB=6m,若按图案在三个正六边形中种上花圃.求: