Question

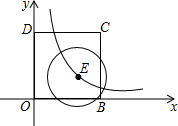如图，平面直角坐标系中，边长为2正方形OBCD的顶点B在x轴正半轴上，点D在y轴正半轴上，半径为1的⊙E的圆心E在双曲线y=

1

x

（x＞0）上移动，当⊙E与正方形OBCD的边相切时，点E的坐标为

 

．

Answer 1

考点：切线的性质,反比例函数图象上点的坐标特征,正方形的性质

专题：计算题

分析：分类讨论：当⊙E与OD相切，如图，根据切线的性质得E点到y轴的距离为1，再根据反比例函数图象上点的坐标特征可确定E点坐标为（1，1），由于正方形OBCD的边长为2，此时⊙E与正方形各边都相切；当点E运动到E′处，⊙E′与BC相切，根据切线的性质得E′点到BC的距离为1，则E′点的横坐标为3，根据反比例函数图象上点的坐标特征易得E′点坐标为（3，

1

3

）；同样可得E″点坐标为（

1

3

，3）．

解答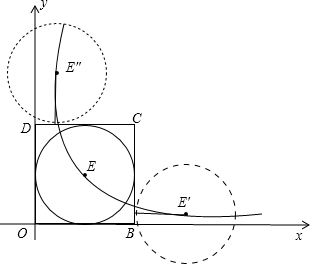：解：当⊙E与OD相切，如图，则E点到y轴的距离为1，所以E点的横坐标为1，
而当x=1时，y=

1

x

=1，此时E点坐标为（1，1），
因为正方形OBCD的边长为2，
所以此时⊙E与正方形各边都相切；
当点E运动到E′处，⊙E′与BC相切，则E′点到BC的距离为1，所以E′点的横坐标为3，
而当x=3时，y=

1

x

=

1

3

，E′点坐标为（3，

1

3

）；
当点E运动到E″处，⊙E″与CD相切，则E″点到DC的距离为1，所以E″点的纵坐标为3，
而当y=3时，

1

x

=3，解得x=

1

3

，E″点坐标为（

1

3

，3）．
综上所述，满足条件的E点坐标为（1，1）、（3，

1

3

）、（

1

3

，3）．
故答案为（1，1）、（3，

1

3

）、（

1

3

，3）．

点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了正方形的性质和反比例函数图象上点的坐标特征．