题目内容
20.如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A、B两点.点A的坐标为(n,6),点B的坐标为(12,1).(1)求反比例函数与一次函数的表达式;
(2)点C为y轴上的一个动点,若S△ACB=15,求点C的坐标.
分析 (1)因为反比例函数y=$\frac{m}{x}$的图象过A(n,6)B(12,1)两点,所以可把B点坐标代入解析式,求得m,写出该函数的解析式,然后再把A点坐标代入,求得n的值,进而写出A点的坐标,再根据待定系数法得到一次函数的解析式;
(2)设点C的坐标为(0,m),连接AC,BC,先求出点P的坐标(0,7),得出PC=|m-7|,根据S△ACB=S△BCP-S△ACP=10,求出m的值,从而得出点C的坐标.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A、B两点.
∴把B(12,1)代入y=$\frac{m}{x}$,得:m=12.
反比例函数的解析式为y=$\frac{12}{x}$;
把A(n,6),代入y=$\frac{12}{x}$得,6=$\frac{12}{n}$,
解得n=2,
把A(2,6),B(12,1)分别代入y=kx+b,
得$\left\{\begin{array}{l}{2k+b=6}\\{12k+b=1}\end{array}\right.$,解得 $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=7}\end{array}\right.$
故一次函数的解析式为y=-$\frac{1}{2}x$+7;
(2)如图,直线AB与y轴的交点为P,设点C的坐标为(0,m),连接AC,BC,
则点P的坐标为(0,7).
∴PC=|m-7|.
∵S△ACB=S△BCP-S△ACP=15,
∴$\frac{1}{2}$×|m-7|×(12-2)=10.
∴|m-7|=2.
∴m1=5,m2=9.
∴点C的坐标为(0,5)或(0,9).
点评 此题考查了反比例函数和一次函数的交点问题,用待定系数法求一次函数和反比例函数的解析式,三角形的面积,解一元一次方程,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

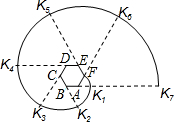 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )| A. | $\frac{2016π}{2}$ | B. | $\frac{2016π}{3}$ | C. | $\frac{2016π}{4}$ | D. | $\frac{2016π}{6}$. |
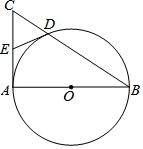 如图,在Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,连接DE.
如图,在Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,连接DE. 某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
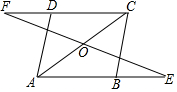 已知:如图,在?ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.
已知:如图,在?ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.