题目内容

10．定义：有三个内角相等的四边形叫三等角四边形．三等角四边形ABCD中，∠A=∠B=∠C，则∠A的取值范围60°＜∠A＜120°．

分析 根据四边形的内角和是360°，且0°＜∠D＜180°，求得∠A+∠B+∠C的范围即可求解．

解答 解：∵四边形的内角和是360°，0°＜∠D＜180°，
∴180°＜∠A+∠B+∠C＜360°，
又∵∠A=∠B=∠C，
∴60°＜∠A＜120°．
故答案是：60°＜∠A＜120°．

点评 本题考查了多边形的内角和，注意到∠D的范围是解题的关键．

练习册系列答案
相关题目
7．如图，抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6．
（1）求抛物线的解析式及点D的坐标；
（2）连接BD，F为抛物线上一动点，当∠FAB=∠EDB时，求点F的坐标；
（3）平行于x轴的直线交抛物线于M、N两点，以线段MN为对角线作菱形MPNQ，当点P在x轴上，且PQ=$\frac{1}{2}$MN时，求菱形对角线MN的长．
1．（1）计算：（π-$\sqrt{3}$）0-|$-\frac{2}{5}$|×$（-\frac{2}{5}）$-1-（-1）2007-（$\frac{1}{2}$）-3
（2）解方程：$\frac{12}{{x}^{2}-9}$-$\frac{2}{x-3}$=$\frac{1}{x+3}$．
18．如图，已知圆锥的底面半径OB为1，高所在直线AO与母线AB的夹角为30°．圆锥的侧面积为2π．
5．已知不等式5x-2＜6x+1的最小整数解是方程$\frac{x}{3}$-$\frac{3ax}{2}$=6的解，则a的值是$\frac{20}{9}$．
15．函数y=-$\frac{1}{x+2}$中自变量x的取值范围是x≠-2．
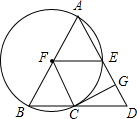2．如图，在△ABD中，AB=AD，以AB为直径的⊙F交BD于点C，交AD于点E，CG⊥AD于点G，连接FE，FC．
（1）求证：GC是⊙F的切线；
（2）填空：
①若∠BAD=45°，AB=2$\sqrt{2}$，则△CDG的面积为$\frac{1}{2}\sqrt{2}-\frac{1}{2}$．
②当∠GCD的度数为30°时，四边形EFCD是菱形．
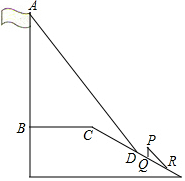19．某中学广场上的旗杆AB，在某一时刻它的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为3米，落在斜坡上的影长CD为2米，AB⊥BC，同一时刻，光线与水平面的夹角为60°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（若结果中有根号，请保留根号）
20．如图，反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A、B两点．点A的坐标为（n，6），点B的坐标为（12，1）．
（1）求反比例函数与一次函数的表达式；
（2）点C为y轴上的一个动点，若S△ACB=15，求点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网