��Ŀ����
1��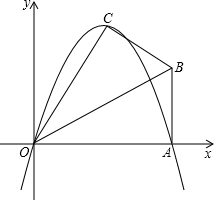 ��֪����Rt��OAB�У���OAB=90�㣬����DΪ����ԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C������C��3��4����
��֪����Rt��OAB�У���OAB=90�㣬����DΪ����ԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C������C��3��4������1������O��C��A����������߽���ʽ��
��2������M����������һ�㣬��λ���߶�OC���Ϸ������M��OC�������룮
��3�����������Ƿ����һ��P��ʹ��OAP=��BOA�������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1������C��CD��x���ڵ�D�����ù��ɶ����ɵ�CO=5��Ȼ������۵������ʿ�֪AO=5�������ô���ϵ��������������ߵĽ���ʽ��
��2������ȷ��OC�Ľ���ʽ������ȷ��ƽ����OC��ֱ�߽���ʽ��Ȼ����������ʽ���ó�����m�ķ��̣������б�ʽΪ0���m��ֵ�������á�OCD��������⣬�ɵý��ۣ�
��3���ֵ�P��x���Ϸ�����P��x���·�����������ۿɵõ�P�����꣮
��� �⣺��1����ͼ��ʾ������C��CD��x���ڵ�D��
��C��3��4����
��DO=3��DC=4��
��CO=5��
�߽�Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
��AO=5��
�������߽���ʽΪ��y=ax2+bx+c��
��$\left\{\begin{array}{l}{c=0}\\{9a+3b+c=4}\\{25a+5b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{10}{3}}\\{c=0}\end{array}\right.$��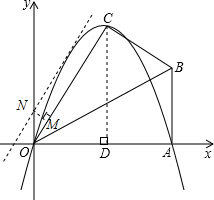
�������߽���ʽΪ��y=-$\frac{2}{3}$x2+$\frac{10}{3}$x��
��2����C��3��4����
��ֱ��OC�Ľ���ʽΪy=$\frac{4}{3}$x��
���M��OC��������ʱ��ƽ����OC��ֱ�߽���ʽΪy=$\frac{4}{3}$x+m��
����$\left\{\begin{array}{l}{y=\frac{4}{3}x+m}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x}\end{array}\right.$��
����δ֪��y��������2x2-6x+3m=0��
��=��-6��2-24m=0��
��ã�m=$\frac{3}{2}$��
���M��OC��������Ϊx��
�ߡ�NOM=��OCD��
��sin��OCD=sin��NOM=$\frac{3}{5}$��
��$\frac{x}{\frac{3}{2}}$=$\frac{3}{5}$��
���x=$\frac{9}{10}$��
��3��AC���е�����Ϊ��4��2����
��ֱ��OB����ʽΪy=$\frac{1}{2}$x��
����$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{17}{4}}\\{{y}_{2}=\frac{17}{8}}\end{array}\right.$��
��P��x���Ϸ�����P������Ϊ��$\frac{3}{4}$��$\frac{17}{8}$����
��P��x���Ϸ���
B��������5��$\frac{5}{2}$����
AP�Ľ���ʽΪy=$\frac{1}{2}$x-$\frac{5}{2}$��
����$\left\{\begin{array}{l}{y=\frac{1}{2}x-\frac{5}{2}}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=5}\\{{y}_{1}=0}\end{array}\right.$����ȥ����$\left\{\begin{array}{l}{{x}_{2}=-\frac{3}{4}}\\{{y}_{2}=-\frac{23}{8}}\end{array}\right.$��
��P��������-$\frac{3}{4}$��-$\frac{23}{8}$����
��������������һ��P��$\frac{3}{4}$��$\frac{17}{8}$����-$\frac{3}{4}$��-$\frac{23}{8}$����ʹ��OAP=��BOA��
���� ���⿼���˶��κ������ۺ�Ӧ�ã��漰��ͼ�εķ��۱任�����ô���ϵ������һ�κ��������κ����Ľ���ʽ��ֱ���������ߵĽ������֪ʶ������һ�����ۺ������Ѷȣ�����ʱҪע�����ν��˼���뷽��˼���Ӧ�ã�

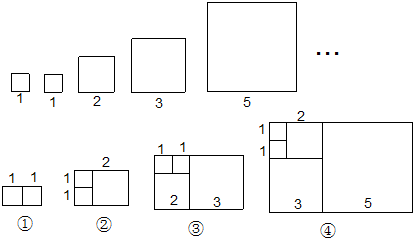
�ٷֱ����δ�����ȡ2����3����4����5��������ƴ�ɾ��β���Ϊ�١��ڡ��ۡ��ܣ���Ӧ���ε��ܳ������ʾ��
| ��� | �� | �� | �� | �� |
| �ܳ� | 6 | 10 | 16 | 26 |
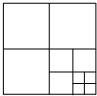 ��ͼ����һ��������ֽƬ�����ĸ�С�����Σ�Ȼ�����е�һ���������ټ����ĸ�С�����Σ��ٽ����е�һ�������μ����ĸ�С�����Σ���˼�����ȥ����������������ϲ��������õ��������εĸ����Ĺ�����ɸ��⣮
��ͼ����һ��������ֽƬ�����ĸ�С�����Σ�Ȼ�����е�һ���������ټ����ĸ�С�����Σ��ٽ����е�һ�������μ����ĸ�С�����Σ���˼�����ȥ����������������ϲ��������õ��������εĸ����Ĺ�����ɸ��⣮��1�����±���д������
| ��������N | 1 | 2 | 3 | 4 | 5 | �� | n |
| ������� | 4 | 7 | 10 | an |
��3�����������������ܷ�õ�2015�������Σ�����ܣ������n��������ܣ���������ɣ�