题目内容
16.把一张圆纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则弧AB的度数是( )
| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
分析 连接OA、OB,作OM⊥AB于M,如图,利用折叠的性质得OM等于半径的一半,再在Rt△OAM中利用三角函数可得到∠A=30°,然后根据等腰三角形的性质和三角形内角和求出∠AOB的度数,再利用圆心角、弧、弦的关系得到弧AB的度数.
解答 解:连接OA、OB,作OM⊥AB于M,如图,
根据折叠的性质得OM=$\frac{1}{2}$OA,
在Rt△OAM中,∵sinA=$\frac{OM}{OA}$=$\frac{1}{2}$,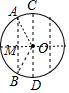
∴∠A=30°,
∵OA=OB,
∴∠B=∠A=30°,
∴∠AOB=120°,
∴弧AB的度数是120°.
故选A.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
6.下列由左到右的变形,属于因式分解的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4x-2=x(x+4)-2 |
7.当式子|x-1|+|x-2|+|x-3|+…+|x-9|取得最小值时,实数x的值等于( )
| A. | 1 | B. | 5 | C. | 6 | D. | 9 |
1.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | $\root{3}{27}$ | D. | $\sqrt{16}$ |
8.若2x=5y,则下列式子中错误的是( )
| A. | $\frac{y}{x}$=$\frac{5}{2}$ | B. | $\frac{y}{x}$=$\frac{2}{5}$ | C. | $\frac{x+y}{x}$=$\frac{7}{5}$ | D. | $\frac{x-y}{y}$=$\frac{3}{2}$ |