题目内容
在平面直角坐标系中,以O为圆心的圆过点A(0,-4),则点B(-2,3)与⊙O的位置关系是( )
| A、在圆内 | B、在圆外 |
| C、在圆上 | D、无法确定 |
考点:点与圆的位置关系,坐标与图形性质
专题:
分析:由已知条件可知圆的半径为4,再根据勾股定理可求出OB的长,和圆的半径4比较大小即可判断点B和⊙O的位置关系.
解答:解:∵以O为圆心的圆过点A(0,-4),
∴圆的半径r=4,
∵点B(-2,3),
∴OB=
=
<4,
∴点B(-2,3)与⊙O的位置关系是在圆内,
故选A.
∴圆的半径r=4,
∵点B(-2,3),
∴OB=
| 22+32 |
| 13 |
∴点B(-2,3)与⊙O的位置关系是在圆内,
故选A.
点评:本题考查了点与圆的位置关系的判断.解决此类题目的关键是首先确定点与圆心的距离,然后与半径进行比较,进而得出结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,它最少和最多需要的立方块是多少( )
用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,它最少和最多需要的立方块是多少( )| A、8与14 | B、10与12 |
| C、9与13 | D、无法确定 |
在代数式2x2y、-5、
、a中,单项式的个数是( )个.
| m+n |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
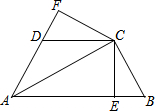 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD, 已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.