��Ŀ����
��ͼ1��������y=ax2+bx+c��a��0���Ķ���ΪM��ֱ��y=m��x��ƽ�У����������߽��ڵ�A��B������AMBΪ����ֱ�������Σ����ǰ���������A��B����֮��IJ������߶�ABΧ�ɵ�ͼ�γ�Ϊ�������߶�Ӧ�����Σ��߶�AB��Ϊ����������M��Ϊ��������M���߶�AB�ľ����Ϊ���ߣ�
��1��������y=
x2��Ӧ�ĵ���Ϊ ��������y=4x2��Ӧ�ĵ���Ϊ ��������y=ax2��a��0����Ӧ�ĵ���Ϊ ��������y=a��x-2��2+3��a��0����Ӧ�ĵ���Ϊ ��
��2��������y=ax2-4ax-
��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��
��3����������y=anx2+bnx+cn��an��0���Ķ�Ӧ���μ�ΪFn��n=1��2��3����������F1��F2������FnΪ�������Σ���Ӧ�ĵ���֮�ȼ�Ϊ���Ʊȣ���Fn��Fn-1�����Ʊ�Ϊ
����Fn�ĵ�����Fn-1�ĵ������е㣬�ֽ���2������õ�������Ϊy1�����Ӧ�����μ�ΪF1��
����������y2�ı���ʽ��
����F1�ĵ���Ϊh1��F2�ĵ���Ϊh2����Fn�ĵ���Ϊhn����hn= ��Fn�ĵ����Ҷ˵������Ϊ ��F1��F2������Fn�ĵ����Ҷ˵��Ƿ���һ��ֱ���ϣ����ǣ�ֱ��д����ֱ�ߵı���ʽ�������ǣ���˵�����ɣ�
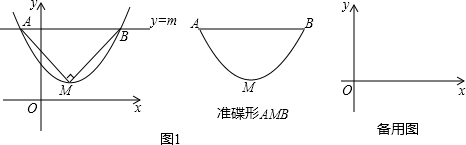
��1��������y=
| 1 |
| 2 |
��2��������y=ax2-4ax-
| 5 |
| 3 |
��3����������y=anx2+bnx+cn��an��0���Ķ�Ӧ���μ�ΪFn��n=1��2��3����������F1��F2������FnΪ�������Σ���Ӧ�ĵ���֮�ȼ�Ϊ���Ʊȣ���Fn��Fn-1�����Ʊ�Ϊ
| 1 |
| 2 |
����������y2�ı���ʽ��
����F1�ĵ���Ϊh1��F2�ĵ���Ϊh2����Fn�ĵ���Ϊhn����hn=

���㣺���κ����ۺ���
ר�⣺ѹ����
��������1�����ݶ��������������ֵ��������y=
x2��������y=4x2�ĵ������Ҷ����ö˵㣨��һ���ޣ������������ȣ��ƹ�������ĸ��������y=ax2��a��0�������ƣ���������y=a��x-2��2+3��a��0��Ϊ����ʽ���ɿ���y=ax2ƽ�Ƶõ������ֵ���ֻ��a�йأ�
��2�����ݣ�1���Ľ��ۣ����ݵ�����a��ֵ��
��3������y1������y2���ڽ�ϻ�ͼ����֪h1��h2��h3������hn-1��hn����ֱ��x=2�ϣ���֤����Ҫ��һ���ƹ㣬���Կ���hn��hn-1���Ҷ���Fn-1�ĵ����е㣬�����ɵã�����ͼʱ��֪�����й��ɵݼ�����������Ҳ�ɵ��Ҷ˵���ص㣮���ڡ�F1��F2������Fn�ĵ����Ҷ˵��Ƿ���һ��ֱ���ϣ��������д�����ж˵�����ƺ����ѣ��ҹ��ɸ��ѣ����Կ��Կ��ǻ����ļ���ͼ�ι�ϵ���������3���㹹�ɵ������߶β����ߣ�����۲�������������۳�������ֱ�߷���ֻ�迼������㼴�ɣ�
| 1 |
| 2 |
��2�����ݣ�1���Ľ��ۣ����ݵ�����a��ֵ��
��3������y1������y2���ڽ�ϻ�ͼ����֪h1��h2��h3������hn-1��hn����ֱ��x=2�ϣ���֤����Ҫ��һ���ƹ㣬���Կ���hn��hn-1���Ҷ���Fn-1�ĵ����е㣬�����ɵã�����ͼʱ��֪�����й��ɵݼ�����������Ҳ�ɵ��Ҷ˵���ص㣮���ڡ�F1��F2������Fn�ĵ����Ҷ˵��Ƿ���һ��ֱ���ϣ��������д�����ж˵�����ƺ����ѣ��ҹ��ɸ��ѣ����Կ��Կ��ǻ����ļ���ͼ�ι�ϵ���������3���㹹�ɵ������߶β����ߣ�����۲�������������۳�������ֱ�߷���ֻ�迼������㼴�ɣ�
����⣺��1��4��
��
��
��
�������£�
��a��0��
��y=ax2��ͼ��������£�
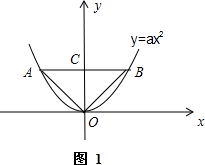
��ع�ԭ��O����ABΪ�������AB��y��Ľ���ΪC������OA��OB��
�ߡ�OABΪ����ֱ�������Σ�AB��x�ᣬ
��OC��AB��
���AOC=��BOC=
��AOB=
•90��=45�㣬
���ACO���BCO��Ϊ����ֱ�������Σ�
��AC=OC=BC��
��xA=yA��xB=yB������y=ax2��
��A��-
��
����B��
��
����C��0��
����
��AB=
��OC=
��
��y=ax2�ĵ���Ϊ
��
��������y=
x2��Ӧ��a=
���õ���
Ϊ4��
��������y=4x2��Ӧ��a=4���õ���Ϊ
Ϊ
��
��������y=ax2��a��0��������Ϊ
��
��������y=a��x-2��2+3��a��0���ɿ���y=ax2����ƽ��2����λ���ȣ�������ƽ��3����λ���Ⱥ�õ���ͼ�Σ�
��ƽ�Ʋ��ı���״����С������
��������y=a��x-2��2+3��a��0��������������y=ax2������
��������y=ax2��a��0��������Ϊ
��
��������y=a��x-2��2+3��a��0��������Ϊ
��
��2����y=ax2-4ax-
=a��x-2��2-��4a+
����
��ͬ��1���������Ϊ
��
��y=ax2-4ax-
�ĵ���Ϊ6��
��
=6��
��� a=
��
��y=
��x-2��2-3��
��3���١�F1�ĵ�����F2�ĵ���=2��1��
��
=
��
��a1=
��
��a2=
��
��y=
��x-2��2-3�ĵ���AB��x���ϣ�A��B��ߣ���
��A��-1��0����B��5��0����
��F2�ĵ�������Ϊ��2��0����
��y2=
��x-2��2��
�ڡ�Fn������Ϊ����ֱ�������Σ�
��Fn�ĵ���Ϊ2hn��
��2hn��2hn-1=1��2��
��hn=
hn-1=��
��2hn-2=��
��3hn-3=��=��
��n+1h1��
��h1=3��
��hn=
��
��hn��hn-1���Ҷ���Fn-1�ĵ����е㣬
��h1��h2��h3������hn-1��hn����һ��ֱ���ϣ�
��h1��ֱ��x=2�ϣ�
��h1��h2��h3������hn-1��hn����ֱ��x=2�ϣ�
��Fn�ĵ����Ҷ˵������Ϊ2+
��
����F1��F2������Fn�ĵ����Ҷ˵���һ��ֱ���ϣ�ֱ��Ϊy=-x+5��
�������£�
����Fn-2��Fn-1��Fn���Σ���ϵ��ͼ2��
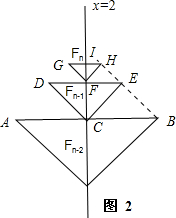
Fn-2��Fn-1��Fn�ĵ����ֱ�ΪAB��DE��GH��C��F��I�ֱ�Ϊ��������е㣬����ֱ��x=2�ϣ������Ҷ˵㣬BE��EH��
��AB��x�ᣬDE��x�ᣬGH��x�ᣬ
��AB��DE��GH��
��GHƽ�������FE��DEƽ�������CB��
���ı���GFEH���ı���DCBE��Ϊƽ���ı��Σ�
��HE��GF��EB��DC��
�ߡ�GFI=
•��GFH=
•��DCE=��DCF��
��GF��DC��
��HE��EB��
��HE��EB����E�㣬
��HE��EB��һ��ֱ���ϣ�
��Fn-2��Fn-1��Fn�ĵ������Ҷ˵�����һ��ֱ�ߣ�
��F1��F2������Fn�ĵ������Ҷ˵�����һ��ֱ�ߣ�
��F1��y1=
��x-2��2-3�����Ҷ˵�����Ϊ��5��0����
F2��y2=
��x-2��2�����Ҷ˵�����Ϊ��2+
��
����
�����ϵ���ɵù������ֱ��Ϊy=-x+5��
��F1��F2������Fn�ĵ������Ҷ˵�����ֱ��y=-x+5�ϣ�
| 1 |
| 2 |
| 2 |
| a |
| 2 |
| a |
�������£�
��a��0��
��y=ax2��ͼ��������£�

��ع�ԭ��O����ABΪ�������AB��y��Ľ���ΪC������OA��OB��
�ߡ�OABΪ����ֱ�������Σ�AB��x�ᣬ
��OC��AB��
���AOC=��BOC=
| 1 |
| 2 |
| 1 |
| 2 |
���ACO���BCO��Ϊ����ֱ�������Σ�
��AC=OC=BC��
��xA=yA��xB=yB������y=ax2��
��A��-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
��AB=
| 2 |
| a |
| 1 |
| a |
��y=ax2�ĵ���Ϊ
| 2 |
| a |
��������y=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a |
��������y=4x2��Ӧ��a=4���õ���Ϊ
| 2 |
| a |
| 1 |
| 2 |
��������y=ax2��a��0��������Ϊ
| 2 |
| a |
��������y=a��x-2��2+3��a��0���ɿ���y=ax2����ƽ��2����λ���ȣ�������ƽ��3����λ���Ⱥ�õ���ͼ�Σ�
��ƽ�Ʋ��ı���״����С������
��������y=a��x-2��2+3��a��0��������������y=ax2������
��������y=ax2��a��0��������Ϊ
| 2 |
| a |
��������y=a��x-2��2+3��a��0��������Ϊ
| 2 |
| a |
��2����y=ax2-4ax-
| 5 |
| 3 |
| 5 |
| 3 |
��ͬ��1���������Ϊ
| 2 |
| a |
��y=ax2-4ax-
| 5 |
| 3 |
��
| 2 |
| a |
��� a=
| 1 |
| 3 |
��y=
| 1 |
| 3 |
��3���١�F1�ĵ�����F2�ĵ���=2��1��
��
| 2 |
| a1 |
| 4 |
| a2 |
��a1=
| 1 |
| 3 |
��a2=
| 2 |
| 3 |
��y=
| 1 |
| 3 |
��A��-1��0����B��5��0����
��F2�ĵ�������Ϊ��2��0����
��y2=
| 2 |
| 3 |
�ڡ�Fn������Ϊ����ֱ�������Σ�
��Fn�ĵ���Ϊ2hn��
��2hn��2hn-1=1��2��
��hn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��h1=3��
��hn=
| 3 |
| 2n-1 |
��hn��hn-1���Ҷ���Fn-1�ĵ����е㣬
��h1��h2��h3������hn-1��hn����һ��ֱ���ϣ�
��h1��ֱ��x=2�ϣ�
��h1��h2��h3������hn-1��hn����ֱ��x=2�ϣ�
��Fn�ĵ����Ҷ˵������Ϊ2+
| 3 |
| 2n-1 |
����F1��F2������Fn�ĵ����Ҷ˵���һ��ֱ���ϣ�ֱ��Ϊy=-x+5��
�������£�
����Fn-2��Fn-1��Fn���Σ���ϵ��ͼ2��

Fn-2��Fn-1��Fn�ĵ����ֱ�ΪAB��DE��GH��C��F��I�ֱ�Ϊ��������е㣬����ֱ��x=2�ϣ������Ҷ˵㣬BE��EH��
��AB��x�ᣬDE��x�ᣬGH��x�ᣬ
��AB��DE��GH��
��GHƽ�������FE��DEƽ�������CB��
���ı���GFEH���ı���DCBE��Ϊƽ���ı��Σ�
��HE��GF��EB��DC��
�ߡ�GFI=
| 1 |
| 2 |
| 1 |
| 2 |
��GF��DC��
��HE��EB��
��HE��EB����E�㣬
��HE��EB��һ��ֱ���ϣ�
��Fn-2��Fn-1��Fn�ĵ������Ҷ˵�����һ��ֱ�ߣ�
��F1��F2������Fn�ĵ������Ҷ˵�����һ��ֱ�ߣ�
��F1��y1=
| 1 |
| 3 |
F2��y2=
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
�����ϵ���ɵù������ֱ��Ϊy=-x+5��
��F1��F2������Fn�ĵ������Ҷ˵�����ֱ��y=-x+5�ϣ�
���������⿼��ѧ������֪ʶ��ѧϰ��������Ӧ����������Ŀ����Ҫ�漰����ֱ�������Σ����κ�������ʽ��ͼ�����ʣ���㹲��֤����֪ʶ���ۺ��ѶȽϸߣ�ѧ������������һ�����ѣ�

��ϰ��ϵ�д�
 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
�����Ŀ
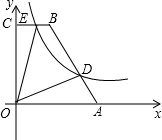 ��ͼ����ֱ������OABC�У�BC��AO����AOC=90�㣬��A��B������ֱ�Ϊ��5��0������2��6������DΪAB��һ�㣬��BD=2AD��˫����y=
��ͼ����ֱ������OABC�У�BC��AO����AOC=90�㣬��A��B������ֱ�Ϊ��5��0������2��6������DΪAB��һ�㣬��BD=2AD��˫����y=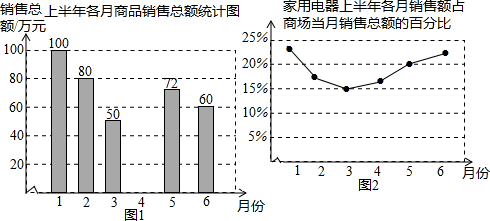
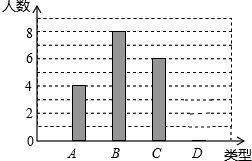 ijУ240��ѧ���μ�ֲ�����Ҫ��ÿ��ֲ��4��7�ã������������20��ѧ��ÿ�˵�ֲ����������Ϊ���ࣺA��4�á�B��5�á�C��6�á�D��7�ã���������������Ƴ���ͼ��ʾ������������ͳ��ͼ���ش��������⣺
ijУ240��ѧ���μ�ֲ�����Ҫ��ÿ��ֲ��4��7�ã������������20��ѧ��ÿ�˵�ֲ����������Ϊ���ࣺA��4�á�B��5�á�C��6�á�D��7�ã���������������Ƴ���ͼ��ʾ������������ͳ��ͼ���ش��������⣺