��Ŀ����
���κ���y=ax2+bx+c����0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����3b+2c��0����4a+c��2b����m��am+b��+b��a��m��1�������н�����ȷ�ĸ����ǣ� ��
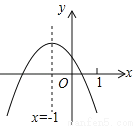
A��1 B��2 C��3 D��4
B�� �������� �����������ͼ����x�����������㣬 ���ax2+bx+c=0����������ȵ�ʵ������ ��b2��4ac��0�� ��4ac��b2��0�� ����ȷ�� �ߩ�=��1�� ��b=2a�� ��a+b+c��0�� ��b+b+c��0��3b+2c��0�� �������ȷ�� �ߵ�x=��2ʱ��y��0�� ��4a��2b+c��0�� ��4a+c��...
��ϰ��ϵ�д�
�����Ŀ


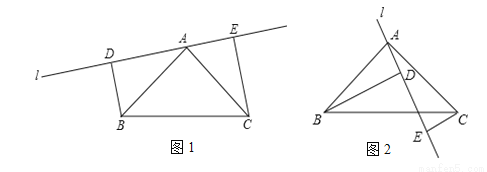
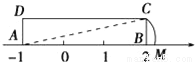
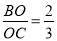 ��AD=10����AO=______��
��AD=10����AO=______��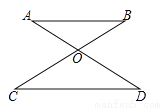
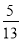 B.
B. 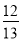 C.
C. 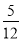 D.
D. 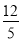
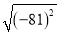 ������ƽ������____��
������ƽ������____��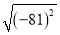 =81����(��9)2=81����81������ƽ������9.
=81����(��9)2=81����81������ƽ������9.