题目内容
1.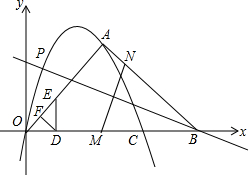 如图,二次函数y=-$\frac{1}{2}$x2+$\frac{7}{2}$x的图象与x轴交于O、C两点,点A在抛物线上,坐标为(5,a),点P是该抛物线位于x轴上方的动点,过点P的直线y=kx-$\frac{35}{3}$k(k≠0)交x轴于点B,连接OA、BA.
如图,二次函数y=-$\frac{1}{2}$x2+$\frac{7}{2}$x的图象与x轴交于O、C两点,点A在抛物线上,坐标为(5,a),点P是该抛物线位于x轴上方的动点,过点P的直线y=kx-$\frac{35}{3}$k(k≠0)交x轴于点B,连接OA、BA.(1)点M、N分别在线段OB、AB上,点M以每秒5个单位长度的速度从点O向点B运动,同时,点N以每秒$\frac{5}{3}$个单位长度的速度从点A向点B运动,当点M、N其中一个点到达点B时,两点同时停止运动,设运动时间为t秒,在运动过程中,当直线PB垂直平分线段MN时,求对应t的值并求出此时点P的横坐标;
(2)在(1)的条件下,当直线PB垂直平分线段MN时,将△BMN沿着直线MN翻折得△B′MN,求△B′MN与△OAB重叠部分的面积;
(3)在x轴上有一点D(2,0),过点D作DE⊥OB交OA于点E,作DF⊥OA于点F,在线段OA上是否存在一点Q,使得△DEF绕点Q旋转180°后,点D、F的对应点D′、F′恰好落在抛物线上?若存在请求出点Q、D′、F′的坐标,若不存在请说明理由.
分析 (1)由题意可知A(5,5),B($\frac{35}{3}$,0),AB=$\frac{25}{3}$,由BM=BN,可得$\frac{25}{3}$-$\frac{5}{3}$t=$\frac{35}{3}$-5t,t=1,推出可得M(5,0),N($\frac{19}{3}$,4),推出MN的中点K坐标($\frac{17}{3}$,2),设直线PB的解析式为y=kx+b,求出PB的解析式解方程组即可解决问题.
(2)如图2中,NB′与OA交于点T,MB′交OA于S,重叠部分是四边形MNTS.想办法求出B′、T、S的坐标,根据S四边形MNTS=S△BMN′-S△STB′计算即可.
(3)根据△ODF是等腰直角三角形,点D(2,0),DF⊥OA,得出点F的坐标,设出Rt△DEF旋转后对应三角形是Rt△D'E'F',由题意可知,F'与A重合,得出F'和Q点的坐标,再根据Rt△DEF≌Rt△D'E'F',DF∥D'F',得出点D'坐标,检验点D′在抛物线上即可.,
解答 解:(1)如图1中,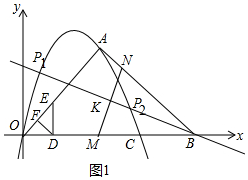
由题意可知A(5,5),B($\frac{35}{3}$,0),AB=$\frac{25}{3}$,
∵PB垂直平分MN,
∴BM=BN,
∴$\frac{25}{3}$-$\frac{5}{3}$t=$\frac{35}{3}$-5t,
∴t=1,
∴可得M(5,0),N($\frac{19}{3}$,4),
∴MN的中点K坐标($\frac{17}{3}$,2),设直线PB的解析式为y=kx+b,则有$\left\{\begin{array}{l}{\frac{17}{3}k+b=2}\\{\frac{35}{3}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=\frac{35}{9}}\end{array}\right.$,
∴直线PB的解析式为y=-$\frac{1}{3}$x+$\frac{35}{9}$,
由$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{7}{2}}\\{y=-\frac{1}{3}x+\frac{35}{9}}\end{array}\right.$,消去y得到9x2-69x+70=0,
解得x=$\frac{23±\sqrt{149}}{6}$,
∴点P的横坐标为$\frac{23±\sqrt{149}}{6}$.
(2)如图2中,NB′与OA交于点T,MB′交OA于S,重叠部分是四边形MNTS.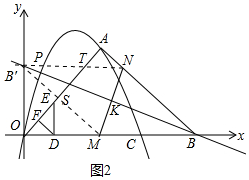
由题意可知B′(-$\frac{1}{3}$,4),M(5,0),N($\frac{19}{3}$,4),B′N∥OB,
∴直线MB′的解析式为y=-$\frac{3}{4}$x+$\frac{15}{4}$,直线OA的矩形为y=x,
∴T(4,4),S($\frac{15}{7}$,$\frac{15}{7}$),
∴S四边形MNTS=S△BMN′-S△B′ST=$\frac{1}{2}$×$\frac{20}{3}$×4-$\frac{1}{2}$×$\frac{7}{3}$×$\frac{13}{7}$=$\frac{67}{6}$.
(3)存在.如图3中,设 Rt△FDE旋转后对应三角形是Rt△F′D′E′.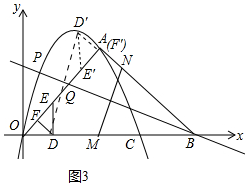
∵△ODF是等腰直角三角形,点D(2,0),DF⊥OA,
∴点F的坐标为(1,1),
由题意可知,F'与A重合
∴点F'的坐标为(5,5),
∵Q点在OA上,且是FA的中点,
∴Q点的坐标为(3,3),
又∵Rt△FDE≌Rt△F′D′E′,DF∥D′F′
∴点D'坐标为(4,6),
把 x=4 代入y=-$\frac{1}{2}$x2+$\frac{7}{2}$x得y=-$\frac{1}{2}$×42+$\frac{7}{2}$×4=6,
∴点M'(4,6)在抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x上,
∴点Q的坐标是(3,3),抛物线上与D、F对应的点的坐标分别是D′(4,6)、F′(5,5).
点评 此题考查了二次函数与一次函数的综合知识,解题的关键是要注意数形结合思想的应用;此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
| A. | 12 | B. | 15 | C. | 12或15 | D. | 45 |
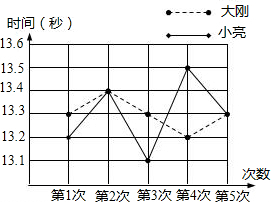
(1)两人每次的成绩(单位:s)
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 大刚 | 13.3 | 13.4 | 13.3 | 13.2 | 13.3 |
| 小亮 | 13.2 | 13.4 | 13.1 | 13.5 | 13.3 |
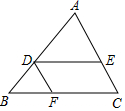 在△ABC中,D,E、F分别在AB、AC、BC上,已知:$\frac{AD}{DB}$=$\frac{AE}{DF}$=$\frac{DE}{BF}$,求证:四边形CFDE是平行四边形.
在△ABC中,D,E、F分别在AB、AC、BC上,已知:$\frac{AD}{DB}$=$\frac{AE}{DF}$=$\frac{DE}{BF}$,求证:四边形CFDE是平行四边形.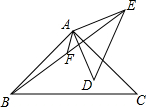 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BE,F是BE的中点,连接AF.若AF=2,AD=5,tan∠DAF=$\frac{3}{4}$,则AB的边为$\frac{37\sqrt{5}}{5}$.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BE,F是BE的中点,连接AF.若AF=2,AD=5,tan∠DAF=$\frac{3}{4}$,则AB的边为$\frac{37\sqrt{5}}{5}$.