题目内容
3.若45°<α<90°,化简$\frac{\sqrt{1-2cosαsinα}}{\sqrt{1-2tanα+ta{n}^{2}α}}$-$\sqrt{1+2cos(90°-α)sin(90°-α)}$+|sinα-sin60°cos45°|分析 先化简二次根式,再根据特殊角三角函数值,可得答案.
解答 解:∵45°<α<90°,
∴$\frac{\sqrt{1-2cosαsinα}}{\sqrt{1-2tanα+ta{n}^{2}α}}$-$\sqrt{1+2cos(90°-α)sin(90°-α)}$+|sinα-sin60°cos45°|
=$\frac{|sinα-cosα|}{|1-tanα|}$-|sinα+cosα|+|sinα-$\frac{\sqrt{6}}{4}$|
=$\frac{sinα-cosα}{tanα-1}$-sinα-cosα+sinα-$\frac{\sqrt{6}}{4}$
=cosα-sinα-cosα+sinα-$\frac{\sqrt{6}}{4}$
=-$\frac{\sqrt{6}}{4}$.
点评 此题考查了特殊角的三角函数值,应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列语句中,正确的是( )
| A. | 若∠α+∠β=180°,则∠α是补角 | |
| B. | 若∠AOB+∠BOC=180°,则∠AOC是直角 | |
| C. | 若∠α与∠β互为补角,则∠α与∠β中必有一个为锐角,另一个角为钝角 | |
| D. | 若∠α与∠β互为余角,则∠α+∠β=90° |
 如图所示的正方形网格中一共有20个长方形.
如图所示的正方形网格中一共有20个长方形.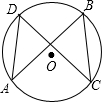 如图所示,在⊙O中,A,B,C,D是⊙O上的四个点,弦AB=CD,求证:AD=BC.
如图所示,在⊙O中,A,B,C,D是⊙O上的四个点,弦AB=CD,求证:AD=BC.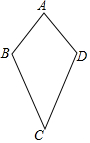 如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( )
如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( )