题目内容
18.化简代数式$\frac{{x}^{2}}{{x}^{2}+2x}$÷$\frac{x-1}{x}$,并判断当x满足不等式组$\left\{\begin{array}{l}{x+2<1}\\{2(x-1)>-6}\end{array}\right.$时代数式的符号.分析 直接解不等式,进而得出x的取值范围,再利用分式的乘除运算法则化简求出答案.
解答 解:∵x满足不等式组$\left\{\begin{array}{l}{x+2<1}\\{2(x-1)>-6}\end{array}\right.$,
∴解得:-2<x<-1,
$\frac{{x}^{2}}{{x}^{2}+2x}$÷$\frac{x-1}{x}$,
=$\frac{x}{x+2}$×$\frac{x}{x-1}$
=$\frac{{x}^{2}}{(x+2)(x-1)}$
则x2>0,x+2>0,x-1<0,
故(x+2)(x-1)<0,
则代数式$\frac{{x}^{2}}{{x}^{2}+2x}$÷$\frac{x-1}{x}$<0.
点评 此题主要考查了分式的乘除运算以及解不等式组,正确得出x的取值范围是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图是分别写有1-9数字的9张牌,让你对调其中的两张牌的位置,使其竖、横、斜每3张牌的数字总和一样大,那么你要对调哪两张牌( )
如图是分别写有1-9数字的9张牌,让你对调其中的两张牌的位置,使其竖、横、斜每3张牌的数字总和一样大,那么你要对调哪两张牌( )
 如图是分别写有1-9数字的9张牌,让你对调其中的两张牌的位置,使其竖、横、斜每3张牌的数字总和一样大,那么你要对调哪两张牌( )
如图是分别写有1-9数字的9张牌,让你对调其中的两张牌的位置,使其竖、横、斜每3张牌的数字总和一样大,那么你要对调哪两张牌( )| A. | 4、6 | B. | 2、8 | C. | 5、2 | D. | 3、7 |
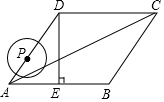 如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2.
如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2.