题目内容
12.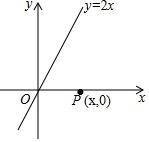 如图,已知直线y=2x和x轴上一动点P(x,0).
如图,已知直线y=2x和x轴上一动点P(x,0).(1)当点P到直线y=2x的距离为2时,求点P的坐标;
(2)若设直线y=2x向上平移一个单位长度后的直线为a,点P(x,0)到直线a的距离为m,试求出m与x之间的关系.
分析 (1)根据点到直线的距离公式,可得答案;
(2)根据点到直线的距离公式,可得答案.
解答 解:(1)直线的解析式为2x-y=0,
P到直线的距离为$\frac{|2x-0|}{\sqrt{{2}^{2}+(-1)^{2}}}$=2,
解得x=$\sqrt{5}$或x=-$\sqrt{5}$,
P点坐标为($\sqrt{5}$,0)或(-$\sqrt{5}$,0);
(2)平移后的解析式为y=2x+1,
2x-y+1=0,
P到直线的距离为$\frac{|2x-0+1|}{\sqrt{{2}^{2}+(-1)^{2}}}$=m,
m=$\frac{2\sqrt{5}}{5}$x或m=-$\frac{2\sqrt{5}}{5}$x.
点评 本题考查了一次函数图象与几何变换,解(1)的关键是利用点到直线的距离公式;解(2)的关键是利用函数图象的平移规律,又利用了点到直线的距离公式.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
15.某机器人公司为扩大经营,决定购进6台机器用于生产某种小机器人.现有甲、乙两种机器供选择,其中每台机器的价格和日生产量如下表所示.经过预算,本次购买机器的费用不能超过34万元.
(1)按要求该公司有几种购买方案?
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?
| 甲种机器 | 乙种机器 | |
| 价格/(万元/台) | 5 | 7 |
| 每台机器的日生产量/个 | 60 | 100 |
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?
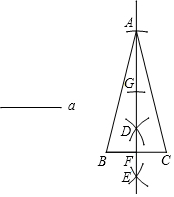 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.