题目内容
【题目】在平面直角坐标系中,抛物线![]() 经过原点
经过原点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,顶点为
,顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() .
.

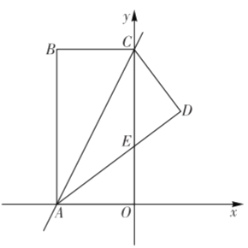
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 为抛物线在第一象限上一点,连接
为抛物线在第一象限上一点,连接![]() 交对称轴于点
交对称轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,不要求写出自变量的取值范围;
之间的函数解析式,不要求写出自变量的取值范围;
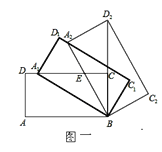
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 横坐标
横坐标![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)代入点(0,0),先求出a的值,然后将二次函数配成顶点式,求出点D坐标;
(2)过点P作x轴垂线,交x轴于点K,ED交x轴于点B;设点![]() ,△PKO∽△EBO,可得到EB的长,加上BD的长即为ED的长;
,△PKO∽△EBO,可得到EB的长,加上BD的长即为ED的长;
(3)如下图,连接AG、AE,过点B、G分别作AG、x轴垂线,交于点M、N.先利用Rt△BGM求得BM、GM的长,在利用Rt△ABM得到tan∠BAG,然后结合Rt△ANG得到AN、GN的长,从而推导出ON的长,接着便可证△OGB是直角三角形,从而推导出∠EOB=30°,得出结论
(1)∵抛物线过点(0,0),代入抛物线得:
0=0-0+28a-7,解得:![]()
则抛物线为:![]()
∴![]()
(2)如下图,过点P作x轴垂线,交x轴于点K,ED交x轴于点B
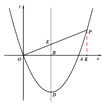
设![]()
∴PK=![]() ,OK=t
,OK=t
∵![]()
∴![]()
∴OB=![]()
∵PK∥EB,∴△PKO∽△EBO
∴![]() ,即:
,即: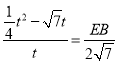
解得:![]()
∴![]()
(3)如下图,连接AG、AE,过点B、G分别作AG、x轴垂线,交于点M、N
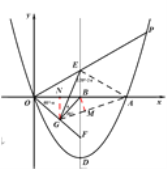
设![]() ,∠GEA=120°
,∠GEA=120°![]()
∵EB是AO的垂直平分线,∴EA=EO,∴![]()
∴在△GEA中,∠EGA=∠EAG=![]()
∴∠BGA=30°
∵抛物线解析式为:![]()
可得:AB=2![]() ,OB=2
,OB=2![]()
∵BG=2![]() ,∴在Rt△BGM中,BM=
,∴在Rt△BGM中,BM=![]() ,GM=3
,GM=3
∴在Rt△ABM中,MA=5
∴![]()
∵AG=3+5=8
∴在Rt△AGN中,GN=![]() ,AN=
,AN=![]()
∴NB=AN-AB=![]() ,∴ON=OB-BN=
,∴ON=OB-BN=![]()
∴在Rt△ONG中,OG=4
∴在△OGB中,三边满足勾股定理逆定理,即∠BGO=90°
∴![]() ,
,![]()
∵![]() ,OB=2
,OB=2![]() ,∠EOB=30°
,∠EOB=30°
∴![]() EB=OB,即
EB=OB,即![]() (
(![]() t-14)=
t-14)=![]()
解得:![]()

【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
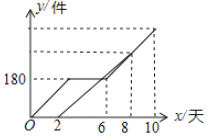
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.

【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
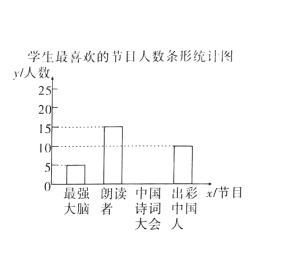
根据以上提供的信息.解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 补全上面的条形统计图;
补全上面的条形统计图;
![]() 名女同学.其余为男同学,现要从中随机抽取
名女同学.其余为男同学,现要从中随机抽取![]() 名同学代表学校参加市里组织的竞赛活动,请求出所抽取的
名同学代表学校参加市里组织的竞赛活动,请求出所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.