Question

【题目】已知：抛物线经过坐标原点．

（1）求抛物线的解析式和顶点B的坐标；

（2）设点A是抛物线与x轴的另一个交点且A、C两点关于y轴对称，试在y轴上确定一点P，使PA+PB最短，并求出点P的坐标；

（3）过点A作AD∥BP交y轴于点D，求到直线AP、AD、CP距离相等的点的坐标．

Answer 1

【答案】（1）抛物线的解析式是y＝﹣x2+2x，顶点B的坐标是（，3）；（2）点P的坐标是（0，2）；（3）到直线AP、AD、CP距离相等的点的坐标是（0，0）和（2，2）．

【解析】

（1）根据抛物线经过原点求出k的值，即可求出解析式，在求顶点坐标即可；

（2）先找出P的位置，再求直线BC的解析式，再求点P的坐标即可；

（3）先求得y轴是∠APC的角平分线，x轴是∠DAP的角平分线，交点符合要求，∠DAP的外角∠EAP的平分线和∠CPA的外角∠FPA的平分线的交点M也符合要求.

解：（1）∵抛物线经过坐标原点，

∴k2+k＝0，

解得：k＝0（舍去），k＝﹣1，

∴抛物线的解析式是y＝﹣x2+2x，

∴y＝﹣x2+2x，

＝﹣（x﹣）2+3，

∴顶点B的坐标是（，3），

答：抛物线的解析式是y＝﹣x2+2x，顶点B的坐标是（，3）；

（2）当y＝0时﹣x2+2x＝0，

解得：x1＝0，x2＝2，

∴A的坐标是（2，0），

A关于y轴的对称点C的坐标是C（﹣2，0），

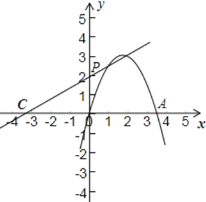
设直线BC的解析式是y＝kx+b，

把B（，3），C（﹣2，0）代入得：，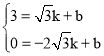

解得：，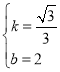

∴直线BC的解析式是y＝x+2，

当x＝0时，y＝2，

∴点P的坐标是（0，2），

答：点P的坐标是（0，2）．

（3）∵A、C关于y轴对称，P在Y轴上，

∴AP＝CP，

∵∠CAP＝∠ACP，x轴⊥y轴，

∴y轴是∠APC的角平分线，

即y轴上任意一点到AP、CP的距离都相等，

∵AD∥PC，

∴∠DAC＝∠ACP，

∴∠DAC＝∠CAP，

∴x轴是∠DAP的角平分线，

即x轴上任意一点到AP、AD的距离都相等，

∴x轴与y轴的交点O到AP、AD、CP距离相等，

∴点的坐标是（0，0），

如图，

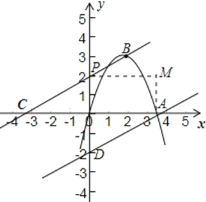
∠DAP的外角∠EAP的平分线和∠CPA的外角∠FPA的平分线的交点M也符合要求，

根据作图条件能得到矩形MAOP，

即点M的坐标是（2，2），

到直线AP、AD、CP距离相等的点的坐标是（0，0）和（2，2），

答：到直线AP、AD、CP距离相等的点的坐标是（0，0）和（2，2）．