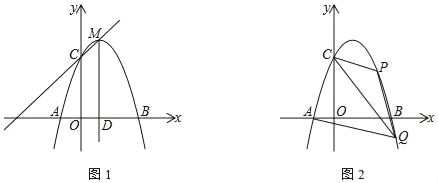Question

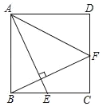
【题目】如图一，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．

（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；

（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，若，求的值．

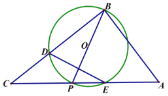
（3）如图二，在（2）的条件下，直线AB上有一点P，BP=2，点E是直线DC上一动点，在BE左侧作矩形BEFG且始终保持，设AB=，试探究点E移动过程中，PF是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在，

【解析】

（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．解直角三角形，求出∠ABA1，得到旋转角即可解决问题；

（2）由△BCE∽△BA2D2，推出，可得CE=，由推出，推出A1C=，推出BH=A1C=，然后由勾股定理建立方程，解方程即可解决问题；

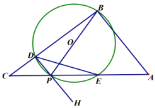
（3）当A、P、F，D，四点共圆，作PF⊥DF，PF与CD相交于点M，作MN⊥AB，此时PF的长度为最小值；先证明△FDG∽△FME，得到，再结合已知条件和解直角三角形求出PM和FM的长度，即可得到PF的最小值.

解：（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．

∴AD=HA1=n=1，

在Rt△A1HB中，∵BA1=BA=m=2，

∴BA1=2HA1，

∴∠ABA1=30°，

∴旋转角为30°，

∵BD=，

∴D到点D1所经过路径的长度=；

（2）∵△BCE∽△BA2D2，

∴，

∴，

∵，

∴，

∴A1C=，

∴BH=A1C=，

∴，

∴m4﹣m2n2=6n4，

∴，

∴（负根已舍去）．

（3）当A、P、F，D，四点共圆，作PF⊥DF，PF与CD相交于点M，作MN⊥AB，此时PF的长度为最小值；

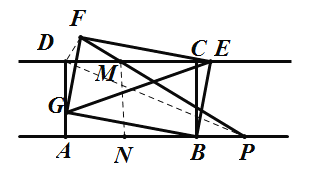
由（2）可知，，

∵四边形BEFG是矩形，

∴，

∵∠DFG+∠GFM=∠GFM+∠MFE=90°，

∴∠DFG=∠MFE，

∵DF⊥PF，即∠DFM=90°，

∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°，

∴∠FDG=∠FME，

∴△FDG∽△FME，

∴，

∵∠DFM=90°，，

∴∠FDM=60°，∠FMD=30°，

∴；

在矩形ABCD中，有，

即，则，

∵MN⊥AB，

∴四边形ANMD是矩形，

∴MN=AD=3，

∵∠NPM=∠DMF=30°，

∴PM=2MN=6，

∴NP=，

∴DM=AN=BP=2，

∴，

∴；