题目内容
7. 如图,抛物线y=-x2+bx+c与x轴分别交于点A(-3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.
如图,抛物线y=-x2+bx+c与x轴分别交于点A(-3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.(1)求抛物线的函数表达式.
(2)判断△ADC的形状,并说明理由.
(3)对称轴DE上是否存在点P,使点P到直线AD的距离与到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)用待定系数法求出抛物线解析式;
(2)先确定出抛物线的顶点坐标,从而求出AD,AC,CD,用勾股定理的逆定理判断即可;
(3)先求出∠ADE的正弦值,再分点P在∠DAB的平分线和∠DAB的外角的平分线两种情况用PM=PE建立方程求解即可.
解答 解(1)∵点A(-3,0),C(0,3)在抛物线y=-x2+bx+c的图象上,
∴$\left\{\begin{array}{l}{-9-3b+c=0}\\{c=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2-2x+3,
(2)由(1)得抛物线解析式为y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点D(-1,4),
∵C(0,3),A(-3,0),
∴AD=2$\sqrt{5}$,AC=3$\sqrt{2}$,CD=$\sqrt{2}$,
∴AD2=AC2+CD2,
∴△ADC是直角三角形;
(3)存在,
理由:∵抛物线解析式为y=-x2-2x+3=-(x+1)2+4,
∴E(-1,0),
∵A(-3,0),D(-1,4),
∴AE=2,DE=4,AD=2$\sqrt{5}$,
在Rt△ADE中,sin∠ADE=$\frac{AE}{AD}$=$\frac{\sqrt{5}}{5}$,
设P(-1,p),
∵点P到直线AD的距离与到x轴的距离相等
①当点P在∠DAB的角平分线时,
如图1,
过点P作PM⊥AD,
∴PM=PD×sin∠ADE=$\frac{\sqrt{5}}{5}$(4-p),PE=p,
∵PM=PE,
∴$\frac{\sqrt{5}}{5}$(4-p)=p,
∴p=$\sqrt{5}$-1,
∴P(-1,$\sqrt{5}$-1),
②当点P在∠DAB的外角的平分线时,
如图2,
过点P作PM⊥AD,
∴PM=PD×sin∠ADE=$\frac{\sqrt{5}}{5}$(4-p),PE=-p,
∴$\frac{\sqrt{5}}{5}$(4-p)=-p,
∴p=-$\sqrt{5}$-1,
∴P(-1,-$\sqrt{5}$-1),
综上所述,存在点P到AD的距离与到x轴的距离相等,点P(-1,$\sqrt{5}$-1)或(-1,-$\sqrt{5}$-1).
点评 此题是二次函数综合题,主要考查了待定系数法,直角三角形的判定,三角函数,三角形的角平分线的性质,解本题的关键是求出∠ADE的正弦值.

| A. | 一定是正整数 | B. | 一定是无理数 | ||
| C. | 一定是负整数 | D. | 可能是有理数,也可能是无理数 |
 观察下列函数y=x,y=x2和y=$\frac{1}{x}$,则给出的下列命题( )
观察下列函数y=x,y=x2和y=$\frac{1}{x}$,则给出的下列命题( )①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
| A. | a≥1 | B. | a≤-1 | C. | a≥-1 | D. | a≥0 |
| A. | 1 | B. | 7 | C. | -1 | D. | -7 |
 如图,在矩形ABCD中,AB=$\sqrt{19}$,AD=8,点P、Q分别是AD边和BC边上的动点,点P从点A向点D运动,点Q从点C向点B运动,且保持CQ=2AP,设AP=x.
如图,在矩形ABCD中,AB=$\sqrt{19}$,AD=8,点P、Q分别是AD边和BC边上的动点,点P从点A向点D运动,点Q从点C向点B运动,且保持CQ=2AP,设AP=x.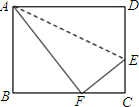 如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm.
如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm.