题目内容
8. 如图,已知AC平分∠BAD,CE⊥AB于E 点,∠ADC+∠B=180°.
如图,已知AC平分∠BAD,CE⊥AB于E 点,∠ADC+∠B=180°.(1)求证:BC=CD;
(2)2AE=AB+AD.
分析 (1)过C作CF⊥AD于F,根据角平分线的性质得:CF=CE,根据AAS证明△FDC≌△EBC可得结论;
(2)由(1)中的全等得:DF=BE,证明Rt△AFC≌Rt△AEC,得AE=AF,根据线段的和与差得出结论.
解答 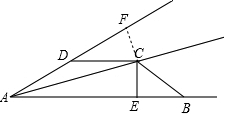 证明:(1)过C作CF⊥AD于F,
证明:(1)过C作CF⊥AD于F,
∵AC平分∠BAD,CE⊥AB,
∴CF=CE,
∵∠ADC+∠CBE=180°,∠ADC+∠FDC=180°,
∴∠CBE=∠FDC,
在△FDC和△EBC中,
∵$\left\{\begin{array}{l}{∠CFD=∠CEB=90°}\\{∠FDC=∠CBE}\\{FC=CE}\end{array}\right.$,
∴△FDC≌△EBC(AAS),
∴CD=BC;
(2)∵△FDC≌△EBC,
∴DF=BE,
在Rt△AFC和Rt△AEC中,
∵$\left\{\begin{array}{l}{AC=AC}\\{CF=CE}\end{array}\right.$,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE,
∴AB+AD=AE+BE+AD=AE+DF+AD=AE+AF=2AE.
点评 本题考查了全等三角形的性质与判定、角平分线的性质,注意利用角平分线性质时,必须是到角两边的垂线段相等,本题是常考题型,难度不大,在证明线段的和与差时,要将线段根据图形中分成和与差,利用全等三角形的对应边相等作等量代换,从而得出结论.

练习册系列答案
相关题目
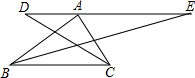 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.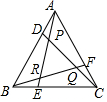 如图,若△ABC为等边三角形,且AD=BE=CF,则∠PQR的度数是60°.
如图,若△ABC为等边三角形,且AD=BE=CF,则∠PQR的度数是60°.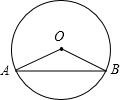 如图,AB是圆O的弦,若∠A=35°,则∠AOB的大小为110度.
如图,AB是圆O的弦,若∠A=35°,则∠AOB的大小为110度.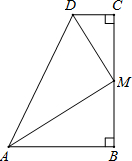 如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:
如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论: